2014-02-09
1189
Задача упаковки в контейнеры
Дано: множество предметов L = {1, …, n } и их веса wi Î(0,1), i Î L.
Найти: разбиение множества L на минимальное число m подмножеств
B 1, B 2, …, Bm такое, что
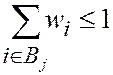, для всех 1 £ j £ m.
Множества Bj называют контейнерами.
Требуется упаковать предметы в минимальное число контейнеров.
Задача NP-трудна и часто возникает в приложениях.
Алгоритм «Следующий подходящий» (NF)
В произвольном порядке упаковываем предметы по следующему правилу. Первый предмет помещаем в первый контейнер.
На k -м шаге пытаемся поместить k -й предмет в текущий контейнер.
Если предмет входит, то помещаем его и переходим к следующему шагу,
иначе помещаем предмет в новый контейнер.
Т = О (n), П = О (1).
Теорема. NF (L) £ 2 OPT (L).
Доказательство. Пусть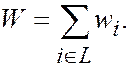 
Так как любые два последовательных контейнера содержат предметы суммарным весом не меньше единицы, то
NF (L) < 2é W ù. Кроме того, OPT (L) ³ é W ù, откуда и следует требуемое.
Пример
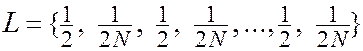. Всего 4 N предметов.
 |  | ||||||||||||||
 | |||||||||||||||
|
| ||||||||||||||
| |||||||||||||||
| |||||||||||||||
|
|
|
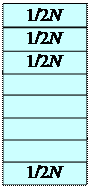Замечание. NF (L) £ 2 OPT (L) – 1 для всех L.
Пусть алгоритм A для множества L порождает A (L) контейнеров и
.
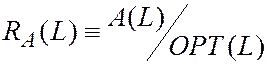Для задачи на минимум гарантированная относительная точность RA для алгоритма A определяется как
RA º inf { r ³ 1 | RA (L) £ r для всех L }.
Определение. Асимптотическая гарантированная относительная точность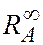 
для алгоритма A определяется как
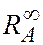º inf { r ³ 1 | $ N > 0 такое, что RA (L) £ r для всех L с OPT (L) ³ N }.
Алгоритм «Первый подходящий» (FF)
В произвольном порядке упаковываем предметы по следующему правилу. Первый предмет помещаем в первый контейнер.
На k -м шаге находим контейнер с наименьшим номером, куда помещается k -й предмет, и помещаем его туда. Если такого контейнера нет, то берем новый пустой контейнер и помещаем предмет в него.
Т = О (n 2), П = О (n).
Теорема. FF (L) £ é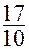
OPT (L) +1ù для всех L и существуют примеры со сколь угодно большими значениями OPT, для которых FF (L) ³ é 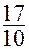OPT (L) – 1ù.
(Без доказательства)
| Пример L = {1,…, 18 m } |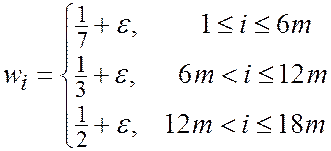 
|
 |
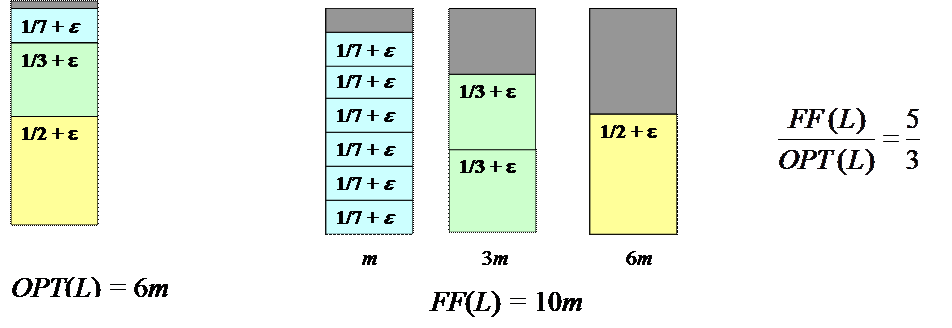Алгоритм «Наилучший подходящий» (BF)
В произвольном порядке упаковываем предметы по следующему правилу. Первый предмет помещаем в первый контейнер.
На k -м шаге размещаем k -й предмет. Находим частично заполненные контейнеры, где достаточно для него свободного места и выбираем среди них наиболее заполненный. Если таких нет, то берем новый пустой контейнер и помещаем k -й предмет в него.
Т = О (n 2), П = О (n).
Теорема. RBF = RFF,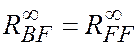 
и существуют примеры со сколь угодно большими значениями OPT(L), длякоторых BF(L) = 4/3 FF(L)
|
|
|
и FF(L) = 3/2 BF(L).
(Без доказательства)
Алгоритмы типа On-line
Предметы поступают в непредсказуемом порядке. Требуется упаковать их в минимальное число контейнеров. Упакованный предмет нельзя перемещать в другой контейнер. Место для предварительного хранения предметов отсутствует.
Алгоритмы NF, FF, BF являются On-line алгоритмами.
Теорема. Для любого On-line алгоритма A справедливо неравенство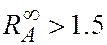 
(Без доказательства)
On-line алгоритм называют алгоритмом с ограниченным доступом к контейнерам, если на каждом шаге алгоритм имеет возможность помещать предметы только в один из K контейнеров (K — const). Эти контейнеры называются открытыми. Если контейнер закрыли, то он уже не открывается (например, отправляется потребителю). Прежде чем добавить пустой открытый контейнер, нужно закрыть один из K открытых контейнеров.
Алгоритм NF — пример для K = 1.
Правила для выбора контейнера
1. Закрыть контейнер с наименьшим номером
2. Закрыть самый заполненный контейнер.
