Лекция №8
Определение. Набор 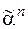 =(a1, a2,…, a n), где a i Î{0,1}, i =1,…, n, называется Булевым (двоичным) набором:
=(a1, a2,…, a n), где a i Î{0,1}, i =1,…, n, называется Булевым (двоичным) набором:
- a i – компоненты набора (координаты вектора),
- n – длина набора (размерность).
Определение. Функция 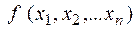 , определенная на множестве
, определенная на множестве 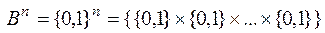 и принимающая значения из множества {0,1}, называется функцией алгебры логики (булевой функцией).
и принимающая значения из множества {0,1}, называется функцией алгебры логики (булевой функцией).
Множество всех булевых функций, зависящих от 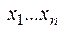 будем обозначать
будем обозначать 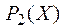 .
.
При n = 0 функция называется ноль местной (const) f =0 или f =1.
В произвольном случае f можно задать таблицей истинности (табл. 8.1), в которой наборы выписываются в порядке возрастания их номеров. Имея в виду такое расположение наборов функцию можно задать вектором ее значений (a1, a2,…, a k), k =2 n.
Таблица 8.1
Табличный способ представления функции
| Координаты вектора | Функция | ||||
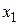
| 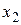
| 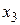
| … | 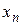
| f |
| … | … | … | … | … | … |
| … |
Количество различных функций n переменных равно числу различных двоичных векторов длины 2 n, т.е. 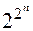 .
.
 2014-02-09
2014-02-09 532
532







