Определение. Функция 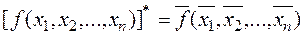 называется двойственной функцией к функции
называется двойственной функцией к функции 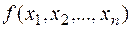 .
.
Правило. Чтобы получить двойственную функцию нужно инвертировать 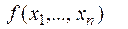
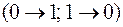 , а затем перевернуть таблицу (табл. 8.4).
, а затем перевернуть таблицу (табл. 8.4).
Таблица 8.4
Пример получения двойственной функции
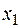
| 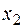
| 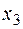
| 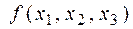
| 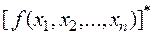
| ||
Соответствие элементарных функций
f 0, 1, x, 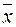 , x 1& x 2, x 1Ú x 2
, x 1& x 2, x 1Ú x 2
f * 1, 0, x, 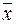 , x 1Ú x 2, x 1& x 2
, x 1Ú x 2, x 1& x 2
Из определения двойственности следует, что
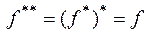 .
.
В качестве аргументов могут быть не только простые переменные xi, но и функции fi (xi).
Теорема. Пусть 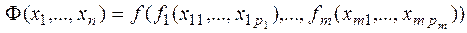 .
.
Тогда 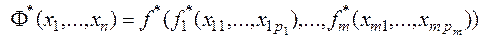 .
.
Доказательство.
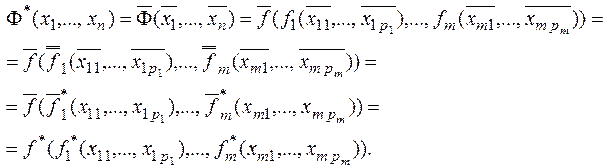
Отсюда вытекает принцип двойственности для функций от функций: двойственной к формуле 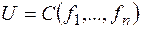 является формула
является формула 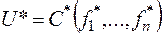 .
.
Пусть формула содержит только символы &, Ú, Ø. Тогда для получения 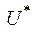 из U нужно заменить:
из U нужно заменить:
на 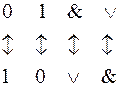
Из принципа двойственности вытекает, что
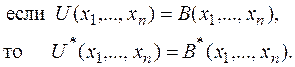
В частности, например,
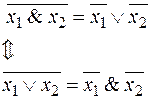 .
.
 2014-02-09
2014-02-09 1219
1219







