2014-02-09
312
Предположим, что рассматриваемая СЛАУ (1) имеет симметричную и положительно определенную матрицу (если это не так, то предварительно СЛАУ надо симметризовать). Значения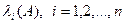 
, заранее известны очень редко, но часто можно сравнительно легко определить границы спектра, т.е. указать такие числа 
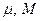, что
.
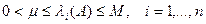Сходимость итерационного процесса (15), (20) будет определяться условием (40), причем, чем меньше будет величина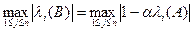 
, тем быстрее будет сходиться итерационный процесс. Уменьшить величину 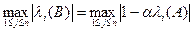можно за счет определенного выбора параметра 
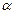. Введем функцию
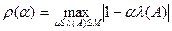. (50)
Рассмотрим задачу минимизации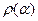 
за счет выбора 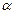. В случае, когда 
, 
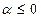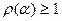, процесс (15), (20) расходится. Пусть 
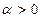. Можно показать, что минимум функции (50) достигается в точке 
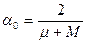и равен 
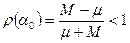. Таким образом, для любой СЛАУ вида (1) можно построить сходящийся МПИ (матрица СЛАУ 
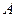предполагается симметричной и положительно определенной (в противном случае СЛАУ сначала симметризуется)):
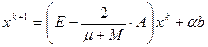. (55)
