Пусть требуется найти функцию u, удовлетворяющую уравнению  и граничному условию
и граничному условию 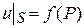 , где P – точки поверхности S.
, где P – точки поверхности S.
Для всякой функции u, непрерывной вместе с первыми производными в замкнутой области T, ограниченной достаточно гладкой поверхностью S и имеющей вторые производные внутри T, имеет место интегральное представление:
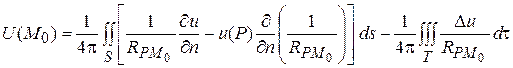 . (1)
. (1)
Если функция u (M) гармоническая, то объемный интеграл равен нулю, если же u (M) удовлетворяет уравнению Пуассона, то объемный интеграл является известной функцией.
Пусть v (M) – некоторая гармоническая функция, непрерывная в 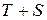 вместе с первыми производными, не имеющая нигде особенностей. Вторая формула Грина
вместе с первыми производными, не имеющая нигде особенностей. Вторая формула Грина
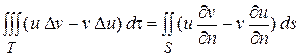
дает:
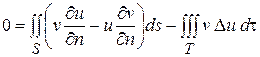 . (2)
. (2)
Складывая (1) и (2), получаем
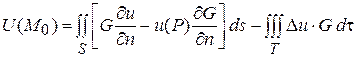 , (3)
, (3)
где
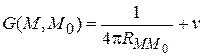
- функция двух точек:  и
и 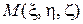 . Точка
. Точка 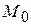 фиксирована, поэтому x, y, z играют роль параметров.
фиксирована, поэтому x, y, z играют роль параметров.
Формула (3) содержит 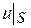 и
и 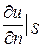 . Между тем, при решении первой краевой задачи задается лишь
. Между тем, при решении первой краевой задачи задается лишь 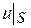 , а при решении второй краевой задачи – значение
, а при решении второй краевой задачи – значение 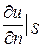 . Функция v выбирается таким образом, чтобы
. Функция v выбирается таким образом, чтобы 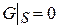 для первой краевой задачи (
для первой краевой задачи (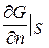 для второй краевой задачи). Определим функцию
для второй краевой задачи). Определим функцию 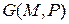 при помощи условий:
при помощи условий:
1. 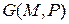 как функция точки
как функция точки 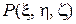 при фиксированной точке
при фиксированной точке 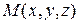 удовлетворяет уравнению Лапласа во всех точках P области T, кроме точки P = M.
удовлетворяет уравнению Лапласа во всех точках P области T, кроме точки P = M.
2. 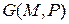 при совпадении аргументов (P = M) обращается в бесконечность.
при совпадении аргументов (P = M) обращается в бесконечность.
3. 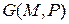 на границе S обращается в нуль, то есть,
на границе S обращается в нуль, то есть, 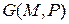 = 0, если
= 0, если 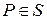 . Этому условию можно удовлетворить, потребовав, чтобы
. Этому условию можно удовлетворить, потребовав, чтобы
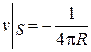 .
.
Функцию 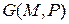 определенную таким образом, будем называть функцией точечного источника(функцией Грина) первой краевой задачи для уравнения Лапласа. Формула (3) дает:
определенную таким образом, будем называть функцией точечного источника(функцией Грина) первой краевой задачи для уравнения Лапласа. Формула (3) дает:
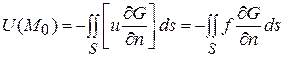 ,
, 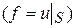
Это и есть решение задачи Дирихле для уравнения Лапласа с помощью функции Грина.
Подведем итог: Функция G определяется при помощи функции v, являющейся решением первой краевой задачи для уравнения 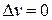 с граничными условиями
с граничными условиями 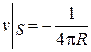 .
.
Функция Грина (источника) 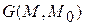 для случая двух измерений, очевидно, будет определяться условиями:
для случая двух измерений, очевидно, будет определяться условиями:
1. 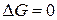 всюду в рассматриваемой области S, кроме точки
всюду в рассматриваемой области S, кроме точки 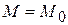 .
.
2. В точке 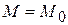 функция G имеет особенность вида
функция G имеет особенность вида
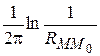 .
.
3. 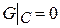 , где C – граница области S. Функция Грина (источника) в этом случае имеет вид
, где C – граница области S. Функция Грина (источника) в этом случае имеет вид
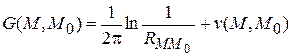 ,
,
где v – всюду непрерывная гармоническая функция, удовлетворяющая на границе условию
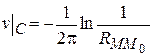 .
.
Решение первой краевой задачи для 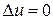 , при этом, дается формулой
, при этом, дается формулой
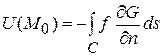
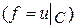 .
.
Функция Грина для сферы (шара)
Пусть дана сфера радиуса R с центром в точке O и 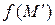 - заданные предельные значения гармонической функции на поверхности сферы, причем
- заданные предельные значения гармонической функции на поверхности сферы, причем 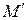 - переменная точка этой поверхности. Мы предполагаем, что
- переменная точка этой поверхности. Мы предполагаем, что 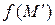 - непрерывная на поверхности сферы функция.
- непрерывная на поверхности сферы функция.
Рассмотрим определенную точку 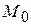 внутри сферы и обозначим через r расстояние от
внутри сферы и обозначим через r расстояние от 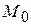 до
до 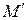 (рис. 10.).
(рис. 10.).
Наряду с точкой 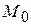 рассмотрим точку
рассмотрим точку 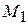 лежащую на продолжении радиуса сферы
лежащую на продолжении радиуса сферы 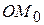 и такую, что
и такую, что
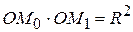 или
или 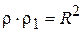 (1)
(1)
Точка 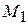 , лежащая вне сферы, называется сопряженной с точкой
, лежащая вне сферы, называется сопряженной с точкой 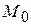 .
.


 M1
M1
r1
r1
 M0
M0
r r
 O M’ (n)
O M’ (n)
R
Рис. 10
Обозначим через 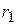 расстояние от точки M до
расстояние от точки M до 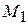 . Если M находится на поверхности сферы в некоторой точке
. Если M находится на поверхности сферы в некоторой точке 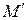 , то величины r и
, то величины r и 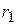 связаны зависимостью. Треугольники
связаны зависимостью. Треугольники 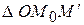 и
и 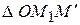 подобны, так как имеют общий угол при вершине O и стороны образующие эти углы пропорциональны в силу (1)
подобны, так как имеют общий угол при вершине O и стороны образующие эти углы пропорциональны в силу (1)
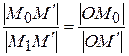 или
или 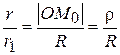
отсюда следует
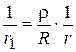 или
или 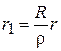 , (2)
, (2)
где 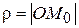 - есть длина
- есть длина 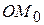 . Так как
. Так как 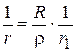 , то можно записать
, то можно записать
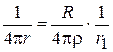 .
.
Рассмотрим функцию 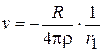 . Эта функция гармоническая всюду кроме точки
. Эта функция гармоническая всюду кроме точки 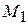 . В частности она гармоническая внутри шара, и на сфере принимает то же значение, что и функция
. В частности она гармоническая внутри шара, и на сфере принимает то же значение, что и функция 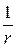 . Отсюда следует, что функцию Грина можно записать следующим образом:
. Отсюда следует, что функцию Грина можно записать следующим образом:
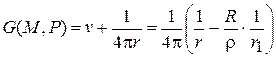 , (3)
, (3)
так как это – гармоническая функция, имеющая в 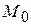 особенность и обращающаяся в нуль на сфере.
особенность и обращающаяся в нуль на сфере.
Найдем нормальную производную от этой функции на поверхности шара
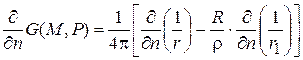 , (4)
, (4)
где n –внешняя нормаль,
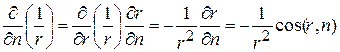 .
.
Для того чтобы определить 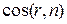 воспользуемся теоремой косинусов:
воспользуемся теоремой косинусов:
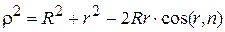
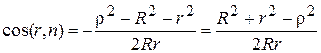
и 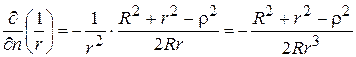 , (5)
, (5)
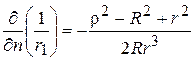 . (6)
. (6)
Учитывая формулы (5) и (6) для нормальной производной функции Грина получим:
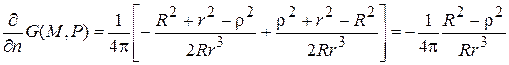 .
.
Таким образом,
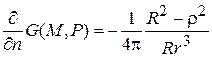 , (7)
, (7)
подставляя это выражение в решение задачи Дирихле, получим
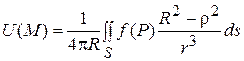 (8)
(8)
Это есть решение задачи Дирихле для шара (для сферы).
Введем сферическую систему координат с началом в центре сферы. Пусть 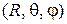 - координаты точки P, а
- координаты точки P, а 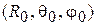 - координаты точки
- координаты точки 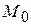 , g - угол между радиус-векторами
, g - угол между радиус-векторами 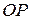 и
и 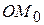 , P – точка на сфере.
, P – точка на сфере.
Тогда формулу (8) можно переписать в виде
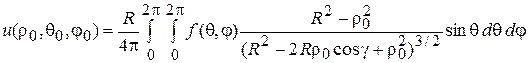 ,
,
где 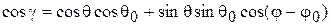 . Эта формула называется интегралом Пуассона для сферы.
. Эта формула называется интегралом Пуассона для сферы.
 2014-02-10
2014-02-10 2105
2105