Основные свойства гармонических функций

Функция, непрерывная со своими производными до второго порядка в некотором объеме и удовлетворяющая там уравнению Лапласа, называется гармонической функцией.

1. Рассмотрим функцию U, гармоническую в ограниченной области D с поверхностью S. Считая, что U непрерывна вместе с производными второго порядка вплоть до S, и применяя вторую формулу Грина (2) к этой функции U и к гармонической функции V = 1, получим, в силу D V = D(1) = 0 и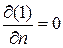

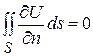, (1)

то есть, имеем первое свойство гармонической функции: интеграл от нормальной производной гармонической функции от поверхности области равен нулю.

2. Если применим к гармонической функции U формулу (3), то, в силу D U = 0, получим:

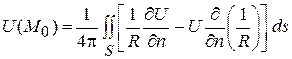. (2)

Это дает нам второе свойство гармонической функции: значение гармонической функции в любой точке внутри области выражается через значения этой функции и ее нормальной производной на поверхности области формулой (2).

3. Применим формулу (2) к сфере с центром в 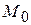и радиусом R, считая, что функция U гармоническая в этой сфере и непрерывна с производными первого порядка вплоть до ее поверхности .

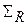В данном случае направление внешней нормали n совпадает с направлением радиуса сферы, так что мы будем иметь

,

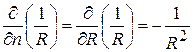и формула (2) дает

.

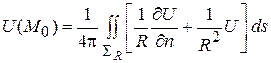Но на поверхности сферы 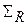величина r имеет постоянное значение R, так что

,

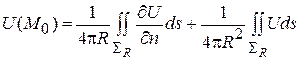или, в силу (1), будем иметь окончательно

.

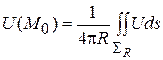Эта формула выражает третье свойство гармонической функции: значение гармонической функции в центре сферы равно среднему арифметическому значению этой функции на поверхности сферы, то есть, равно интегралу от значений функции по поверхности сферы, деленному на площадь этой поверхности.

4. Функция, гармоническая внутри области и непрерывная вплоть до границы области, достигает своего наибольшего и наименьшего значения только на границе области, кроме того случая, когда эта функция есть постоянная.