Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая или одна червонная карта.
Здесь событие А обозначает наступление хотя бы одного из событий Ai, а qi – вероятность противоположных событий.
Обозначим появление хотя бы одной бубновой карты – событие А, появление хотя бы одной червонной карты – событие В. Таким образом нам надо определить вероятность события С = А + В.
Кроме того, события А и В – совместны, т.е. появление одного из них не исключает появления другого.
Всего в колоде 13 червонных и 13 бубновых карт.
При вытаскивании первой карты вероятность того, что не появится ни червонной ни бубновой карты равна 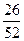 , при вытаскивании второй карты -
, при вытаскивании второй карты -  , третьей -
, третьей - 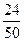 , четвертой -
, четвертой - 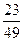 .
.
Тогда вероятность того, что среди вынутых карт не будет ни бубновых, ни червонных равна 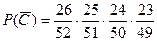 .
.
Тогда 
Вероятность выпадения 6 очков при одном броске кости равна 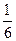 . Вероятность того, что не выпадет 6 очков -
. Вероятность того, что не выпадет 6 очков -  . Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна
. Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна 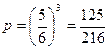 .
.
Тогда вероятность того, что хотя бы один раз выпадет 6 очков равна 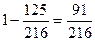 .
.
 2014-02-10
2014-02-10 2746
2746
