ВЕРОЯТНОСТИ СУММЫ И ПРОИЗВЕДЕНИЯ СОБЫ­ТИЙ.

Часто бывает так, что вероятность некото­рого события можно найти, зная вероятности других событий, связанных с этим со­бытием.

Теорема сложения вероятностей.

?Теорема 2.6. (Теорема сложения вероятностей). Вероят­ность суммы (объедине­ния; появления одного из них, безраз­лично какого) двух произвольных событий равна сумме вероят­ностей этих событий за вычетом вероятности их совместного появле­ния, т.е. P (A + B) = P (A) + P (B) - P (AB).

Следствие 1. Вероятность суммы (объединения) попарно не­совместных событий равна сумме их вероятностей, т.е. P (A ₁+ A ₂+...+ A_n) = = P (A ₁) + P (A ₂) +... + P (A_n).

Следствие 2. Пусть A ₁, A ₂,..., A_n – полная группа попарно несовместных собы­тий. Тогда P (A ₁)+ P (A ₂)+... + P (A_n) = 1.

Следствие 3. Сумма вероятностей противоположных собы­тий равна единице, т.е. P (A) + P (` A) = 1.

Пример 2.10. В урне 5 белых, 6 черных и 9 красных шаров. Какова вероятность того, что первый наугад вынутый шар окажется черным или красным?

Решение. Здесь имеется всего 20 элементарных исходов, из кото­рых появлению черного шара бла­гоприятствует 6, а появлению крас­ного - 9. Поэтому вероятность со­бытия A - появление черного шара: P (A) = 6/20, а вероятность события B - появление красного шара: P (A) = 9/20. Поскольку собы­тия A и B несовме­стны (вынимается всего один шар), то P (A + B) = P (A) + P (B) = 6/20 + 9/20 = 0,75. Ответ: 0,75.

? Условная вероятность события B (P_A(B)) - вероятность события B, вычислен­ная при условии, что событие A уже про­изошло. Если A и B – независимые события, то P_A (B) = P (B), P_B (A) = P (A).

Теорема умножения вероятностей.

?Теорема 2.7. (Теорема умножения вероятностей). Вероят­ность произведения (пе­ресечения; совместного появления) двух произвольных событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при усло­вии, что первое собы­тие уже наступило, т.е. P (AB) = P (A)· P_A (B) = P (B)· P_B (A).

Пример 2.11. На полке стоят 11 научно-популярных книг и 5 ху­дожественных. Какова вероят­ность того, что две подряд наугад взятые книги окажутся художественными?

Решение. Рассмотрим два события B ₁ и B ₂: B ₁ - при первом испы­та­нии взята художественная книга, B ₂ - при втором испытании взята ху­дожественная книга. По теореме 2.7 вероятность такого собы­тия равна P (B ₁ B ₂)= P (B ₁)· P_{B 1}(B ₂). Вероятность события B ₁ P (B ₁) = 5/16. По­сле первого испытания на полке останется 15 книг, из которых 4 ху­доже­ственные, по­этому условная веро­ятность P_{B 1}(B ₂) = 4/15. Отсюда искомая вероятность равна: P (B ₁ B ₂) = 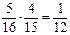. Ответ: 1/12.

Следствие 1. Вероятность совместного появления несколь­ких событий равна про­изведению вероятности одного из них на условные вероят­ности всех остальных, при­чем вероятность ка­ждого последующего события вычис­ляют при условии, что все предыдущие события уже наступили, т.е. P (A ₁· A ₂·...· A_n) = P (A ₁)· P_{A 1}(A ₂) P_{A 1 A 2}(A ₃). ·... · P_{A 1 A 2… An -1}(A_n).

Пример 2.12. Из десяти карточек составлено слово «МАТЕМА­ТИКА». Из них школьник нау­дачу выбирает поочередно четыре кар­точки и приставляет одну к другой. Какова вероятность того, что по­лучится слово «ТЕМА»?

Решение. Введем события A ₁, A ₂, A ₃, A ₄, состоящие в том, что пер­вая выбранная буква - Т, вторая - Е, тре­тья – М и четвертая - А. Нам нужно найти вероят­ность произведения этих событий. По след­ствию 1 из тео­ремы 2.7 имеем:

P (A ₁· A ₂· A ₃· A ₄) = P (A ₁)· P_{A 1}(A ₂)· P_{A 1 A 2}(A ₃)· P_{A 1 A 2 A 3}(A ₄) = 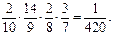Ответ: 1/420.

Следствие 2. Если A ₁, A ₂,..., A_n – независимые события, то ве­роятность их произве­дения (совместного появления) равна про­изведению вероятностей этих собы­тий, т.е. P (A ₁· A ₂·... · A_n) = P (A ₁)· P (A ₂)·... · P (A_n).

Пример 2.13. Два стрелка независимо один от другого де­лают по одному выстрелу по од­ной и той же мишени. Вероятность поражения мишени первым стрелком – 0,7, вторым – 0,8. Какова вероят­ность того, что ми­шень будет поражена?

Решение. Пусть событие А состоит в том, что мишень поразил пер­вый стрелок, а событие В - в том, что ми­шень поразил второй стрелок. По условию Р (А) = 0,7 и Р (В) =0,8.

1-й способ. Рассмотрим противоположные события: `A - промах первого стрелка, `B - промах вто­рого. По следствию 3 из тео­ремы 2.6 получаем Р (`A) = 1-0,7 = 0,3 и Р (`B) = 1-0,8 = 0,2. Произведение собы­тий `A ·`B означает промах обоих стрелков. По смыслу задачи собы­тия А и В являются незави­симыми, поэтому и противоположные со­бытия `A и `B также будут независимыми. По следствию 2 из теоремы 2.7 получаем вероят­ность того, что оба стрелка промахнутся: Р(`А·`В) = 0,3·0,2 = 0,06. Нас же интересу­ет вероятность противоположного события, состоящего в том, что мишень поражена. По­этому искомую вероят­ность мы находим по следствию 3 из теоремы 2.6: 1 - 0,06 = 0,94.

2-й способ. Искомая событие (мишень будет поражена хотя бы од­ним стрелком) есть сумма собы­тий A и B. По теореме 2.6. P (A + B) = P (A) + P (B) - P (AB) = 0,7 + 0,8 – 0,7·0,8 = 1,5 – 0,56 = 0,94. Ответ: 0,94.

Пример 2.14. В студенческой группе 25 человек. Какова вероят­ность того, что дни рождения хотя бы у двоих совпадают?

Решение. Вероятность того, что дни рождения у двух произвольно взятых людей совпадают, равна 1/365 (считаем, что попадания дня рождения на любой день в году - равновозможные случаи). Тогда ве­роятность того, что дни рожде­ния двух людей не совпадают, т.е. веро­ятно­сть противопо­ложного события равна 1-1/365 = 364/365. Вероят­ность того, что день рожде­ния третьего отличается от дней рождения двух предыдущих, составит 363/365 (363 случая из 365 благо­приятст­вуют этому событию). Рассуждая аналогично, находим, что для 25-го члена группы эта веро­ятность равна 341/365. Далее найдем вероят­ность того, что дни рождения всех 25 членов группы не совпадают. По­скольку все эти события (несовпадение дня рождения каждого оче­редного члена группы с днями ро­ждения преды­дущих) независимы, то по следствию 2 из теоремы 2.7 получаем:

P (A ₂ A ₃... A ₂₅) = 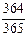· ·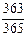... · 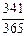» 0,43.

Это вероятность того, что дни рождения у всех 25 человек не сов­падают. Ве­роятность противопо­ложного события будет вероятностью того, что хотя бы у двоих дни рождения совпадают, т.е. иско­мой веро­ятностью P» 1-0,43 = 0,57. Ответ:» 0,57.

Формула полной вероятно­сти.

?Теорема 2.8. Пусть B ₁, B ₂, …, B_n – полная группа попарно не­совместных событий. Ве­роятность события A, которое может наступить лишь при условии наступления од­ного из событий B ₁, B ₂, …, B_n, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность собы­тия A, т.е.

P(A) = P (B ₁)· P_{B 1}(A) + P (B ₂)· P_{B 2}(A) + … + P (B_n)· P_Bn (A).

Эта формула называется формулой полной вероятно­сти. События B ₁, B ₂, …, B_n, удовлетворяющие условию теоремы 2.8, называют гипотезами.

Пример 2.15. Турист равновероятно выбирает один из трех маршру­тов: конный, водный и горный. Вероятность, что он успешно преодолеет путь при выборе конного способа передвижения, равна 0,75, при выборе водного пути – 0,8, при выборе горного маршрута – 0,55. Найдите вероятность, что турист успешно преодолеет весь путь при любом выборе маршрута.

Решение. Введем события: A – «Турист успешно преодолеет весь путь при любом выборе маршрута», B ₁, B ₂, B ₃ – выбран соответственно, конный, водный и горный маршрут. Поскольку выбор маршрута равновероятен, то вероятно­сти выбора каждого маршрута P (B ₁) = P (B ₂) = P (B ₃) = 1/3. По условию P_{B 1}(A) = 0,75; P_{B 2}(A) = 0,8; P_{B 3}(A) = 0,55. Тогда по формуле полной вероятности: P (A) = P (B ₁)· P_{B 1}(A) + P (B ₂)· P_{B 2}(A) + P (B ₃)· P_{B 3}(A) = (1/3)·0,75 + (1/3) ·0,8 + (1/3)0,55 = 0,7.

Ответ: 0,7.

?Теорема 2.9. Условная вероятность любой гипотезы B _i (i = 1, 2, …, n) вычисляется по формуле Бейеса:

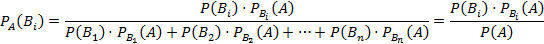
Формула Бейеса позволяет переоценить вероятности гипотез после того, как ста­но­вится известным результат испытания, в итоге которого появилось событие A.

Пример 2.16. Имеется три набора микросхем, первый из которых содержит 100, второй 300 и тре­тий 600 микросхем. Вероятность того, что микросхема, взятая наугад из первого набора, исправна, равна 0,9, а для второго и третьего наборов – соответственно 0,85 и 0,8. Какова вероятность того, что: а) произвольно взятая микросхема исправна: б) исправная микросхема извлечена из второго на­бора?

Решение. а) В данном случае имеется три гипотезы, вероятности которых P (B ₁) = 0,1, P (B ₂) = 0,3, P (B ₃) = 0,6. Пользуясь формулой полной вероятности, находим P (A) = P (B ₁)· P_{B 1}(A) + P (B ₂)· P_{B 2}(A) + P (B ₃)· P_{B 3}(A) = 0,1·0,9 + 0,3·0,85 + 0,6·0,8 = 0,825.

б) Допустим, что искомое событие A произошло – извлечена ис­правная микросхема. Найдем ве­ро­ятность P_A (B ₂) того, что эта микро­схема извлечена из второго набора. Согласно формулы Бейеса,

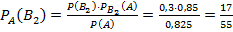Ответ: а) 0,825; б) 17/55.

Пример 2.17. Из 10 учеников, которые пришли на экзамен по ма­тематике, трое подготовились от­лично, четверо – хорошо, двое – удовлетворительно, а один совсем не готовился. В билетах 20 вопро­сов. Отлично подготовившиеся ученики могут ответить на все 20 во­просов, хорошо – на 16 вопросов, удовлетворительно – на 10, и непод­готовившийся – на 5 вопросов. Каждый ученик получает наугад 3 во­проса из 20. Ученик, приглашенный первым, ответил на все 3 вопроса. Какова вероятность того, что он отличник?

Решение. Обозначим события: B ₁ – «Приглашен ученик, подгото­вившийся отлично», B ₂ – «При­глашен ученик, подготовившийся хо­рошо», B ₃ – «Приглашен ученик, подготовившийся удовлетвори­тельно», B ₄ – «Приглашенный ученик к экзамену не готов», A – «При­глашенный ученик ответил на 3 вопроса». Согласно условию задачи P (A ₁) = 0,3, P (A ₂) = 0,4, P (A ₃) = 0,2, P (A ₄) = 0,1. Кроме того, ясно, что P_{B 1}(A) = 1, P_{B 2}(A) = 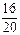··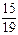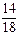» 0,491, P_{B 3}(A) = 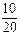··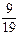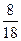» 0,105, P_{B 3}(A) = 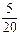··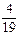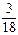» 0,009. Нам необходимо найти P_A (B ₁). По фор­муле Бейеса P_A (B ₁) = 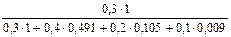» 0,58.

Как видим, искомая вероятность сравнительно не велика, Поэтому учителю придется предложить ученику еще несколько дополнитель­ных вопросов. Ответ: 0,58.