По мере увеличения N частость приближается к вероятности

Зависимость между числовыми значениями случайной величины и вероятностью их появления устанавливается законом распределения вероятностей случайных величин. Закон распределения вероятностей дискретной случайной величины можно представить в виде таблицы или графика, показывающего, с какой вероятностью случайная величина X принимает то или иное числовое значение xi.

Закон распределения вероятностей непрерывной случайной величины, которая может принимать любое значение в пределах заданного интервала нельзя представить в виде таблицы.

Закон распределения представляют в виде дифференциальной функции распределения или плотности распределения вероятности pX (x). Эта функция представляет собой предел отношения вероятности того, что случайная величина X примет значение, лежащее в интервале от x до х + 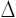x, к величине интервала 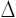х, при 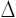х, стремящемся к нулю.

Характер рассеяния достаточно большой совокупности значений случайной величины, как правило, соответствует определённому теоретическому закону распределения.

Рассеяние значений случайной величины, изменение которой зависит от большого числа факторов, когда ни один из факторов не имеет преобладающего влияния, подчиняется закону нормального распределения вероятностей (закону Гаусса), показанного на рис. 3.

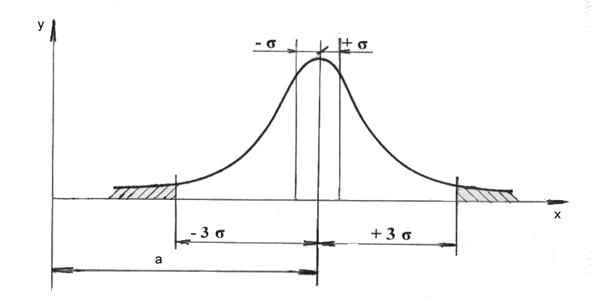
Рис. 3. Кривая плотности вероятности нормального распределения

Этому закону с некоторым приближением может подчиняться: рассеяние погрешностей многократных измерений; рассеяние погрешностей изготовления; погрешности измерения линейных и угловых размеров; массы деталей; величин твердости и других механических и физических величин.

Закон нормального распределения имеет следующие свойства:

· вероятность появления положительных и отрицательных погрешностей одинакова;

· малые по величине погрешности имеют большую вероятность появления, чем большие;

· алгебраическая сумма отклонений от среднего значения равна нулю.

Зависимость плотности вероятности определяется уравнением:

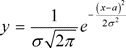(3.2)

где a и 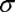- параметры распределения; x - аргумент функции плотности вероятности, т.е. случайная величина, изменяющаяся в пределах - 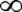< x < + 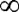; e - основание натуральных логарифмов. Нормальное распределение представляет собой кривую симметричную относительно оси ординат. Величина a равна математическому ожиданию MX случайной величины X, определяемому по формулам:

для дискретной величины

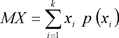(3.3),

где x_i - возможное значение дискретной случайной величины; p (x_i) - вероятность значения x_i дискретной случайной величины;

для непрерывных величин,

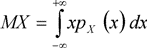(3.4),

где рX (х) - плотность вероятности непрерывной случайной величины X. Значение MX характеризует положение центра группирования случайных величин, около которого располагаются, например, размеры большинства деталей в партии.

При отсутствии систематических погрешностей в результатах многократных измерений одной и той же величины в одних и тех же условиях, математическое ожидание можно рассматривать как наибольшее приближение к истинному значению измеряемой величины.

В качестве математического ожидания при многократных измерениях параметра выступает среднее арифметическое значение х

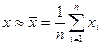(1)

Величину рассеяния значений случайной величины относительно центра группирования определяет параметр 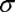, который называют средним квадратическим отклонением случайной величины, его определяют по формулам:

для непрерывной величины

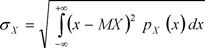(3.6)

для дискретной величины

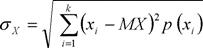(3.5)

или:

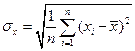при n≥20, 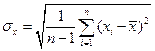при n<20 (2)

Рассеяние случайных величин характеризуется также дисперсией D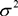X = X.

Случайные погрешности нельзя исключить полностью, но их влияние может быть уменьшено путем обработки результатов измерений. Для этого должны быть известны вероятностные и статистические характеристики (закон распределения, закон математического ожидания, СКО, доверительная вероятность и доверительный интервал). Часто для предварительной оценки закона распределения параметра используют относительную величину СКО — коэффициент вариации:

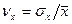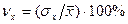или (5)

Например, при ν_х < 0,33,...,0,35 можно считать, что распределение случайной величины подчиняется нормальному закону.

Лекция 7.

Статистические методы обработки измерений (продолжение)

В тоже время существуют другие законы распределения, описывающие случайные величины, природа возникновения которых имеет несколько иной характер.

В рассматриваемом случае необходимо упомянуть закон Максвелла, которому подчиняются существенно положительные величины, например: рассеяние значений эксцентриситета, радиальное и торцевое биения, отклонения от соосности, дисбаланс и другие величин, которые не могут принимать отрицательные значения.

Для оценки надёжности работы изделий используют закон Вейбулла, который даёт представление о вероятности отказов.

Получили распространение также закон Симпсона или закон треугольника и закон равной вероятности.

Однако, для обработки результатов наблюдений в основном применяют закон нормального распределения - закон Гаусса.

Вернемся к распределению вероятностей Гаусса. Формула (3.2) выражает уравнение кривой, если начало отсчета расположено на оси x произвольно. При совпадении центра группирования с началом отсчета величины x уравнение кривой нормального распределения будет иметь вид

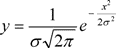(3.7)

Вероятность попадания величины в заданный интервал можно определить следующим образом. Ветви теоретической кривой нормального распределения (рис. 3.3) уходят в бесконечность, асимптотически приближаясь к оси абсцисс. Площадь, ограничиваемая кривой и осью абсцисс, равна вероятности того, что случайная величина, например, погрешность размера, лежит в интервале ±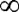. Площадь под кривой распределения равна 1 или 100%, она определяется интегралом

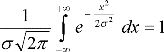(3.8)

Начало координат расположено в точке, совпадающей с центром группирования. Так как подынтегральная функция четная и кривая симметрична относительно максимальной ординаты, можно записать

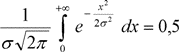(3.9)

Для выражения случайной величины x в долях ее 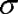примем: x / 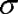= z, откуда x = 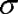z, d x = 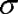d z. В этом случае абсцисса на рис. 3.3 будет выражена в долях 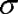. Если принять за пределы интегрирования 0 и z, то интеграл в выражении (3.8) будет функцией z, т.е.

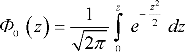(3.10)

Функцию Ф 0 (z) называют нормированной функцией Лапласа: Ф 0 (0) = 0; Ф 0 (- z) = - Ф 0 (z); Ф 0 (- 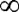) = - 0,5; Ф 0 (+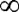) = 0,5.

Из формулы (3.9) и рис. 3.4 следует, что площадь, ограниченная отрезком - z 1 + z 1 оси абсцисс, кривой плотности вероятности и двумя ординатами, соответствующими границам отрезка, представляет собой вероятность попадания случайной величины z 1, в данный интервал.

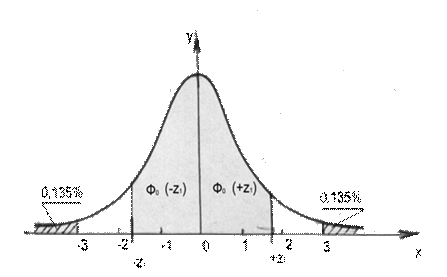
Рис. 4 Кривая нормального распределения и иллюстрация подынтегральных функций

Данные для функции Ф 0 (z) приводятся в справочниках. Пользуясь этими данными можно определить вероятность того, что случайная величина x, выраженная через 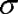, будет находиться в пределах того или иного интервала ± z 1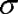. Например, находим, при z 1 = 3, что соответствует случайной величине x = 3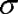, Ф 0 (3) = 0,49865 или Ф 0 (- 3) - Ф 0(3) = 2 Ф 0 (3) = 0,9973.

Так как площадь, ограниченная кривой Гаусса и осью абсцисс, равна 1, то площадь, лежащая за пределами значений х = ± 3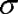, равна 1 - 0,9973 = 0,0027 и расположена симметрично по 0,00135 или по 0,135% справа и слева относительно оси у (см. рис. 3.4).

Следовательно, с вероятностью, близкой к единице, можно утверждать, что случайная величина X не будет выходить за пределы ± 3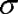. Поэтому при распределении случайной величины по закону Гаусса поле рассеяния, равно V lim = 6 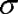или диапазон ± 3 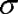считают за практически предельное поле рассеяния случайной величины и принимают за норму точности - допуск. При этом вероятность выхода случайной величины за пределы значений ± 3 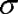равна 0,0027 или 0,27%.

Среднеквадратическое отклонение. Вероятность попадания среднего значения результата измерения в заданный интервал.

Величина среднего значения х, полученная в одной серии измерений, является случайным приближением к х_и. Для оценки ее возможных отклонений от х_и определяют опытное среднее квадратическое отклонение (CKO)

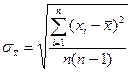(3)

Формулы (2) и (3) соответствуют центральной предельной теореме теории вероятностей, согласно которой

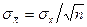(4)

Среднее арифметическое из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения. Это отражает и формула (4), определяющая фундаментальный закон теории погрешностей. Из него следует, что если необходимо повысить точность результата (при исключении систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз и т. д.

Нужно четко разграничивать применение формул (2) и (3): величина (3) используется при оценке погрешностей окончательного результата, а (2) — при оценке погрешности метода измерения.

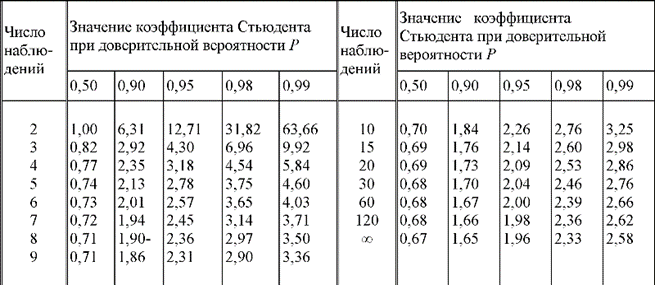
До сих пор рассматривались оценки СКО по "необходимому" (достаточно большому) числу измерений. В этом случае σ² называется генеральной дисперсией. При малом числе измерений (менее 10—20) получают так называемую выборочную дисперсию 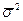. Причем 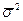→σ² лишь при n→∞. То есть если считать, что 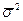=σ², то надежность оценки снижается с уменьшением n, а значения доверительной вероятности Р завышаются.

Поэтому при ограниченном числе измерений n вводят коэффициент Стьюдента t_p, определяемый по специальным таблицам в зависимости от числа измерений и принятой доверительной вероятности Р.

Тогда средний результат измерений находится с заданной вероятностью Р в интервале 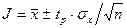и отличается от действительного значения на относительную величину .

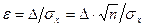Для уменьшения случайной погрешности есть два пути: повышение точности измерений (уменьшение σ_х) и увеличение числа измерений n с целью использования соотношения (2.4). Считая, что все возможности совершенствования техники измерений использованы, рассмотрим второй путь. При этом отметим, что уменьшать случайную составляющую погрешности целесообразно лишь до тех пор, пока общая погрешность измерений не будет полностью определяться систематической составляющей Δ_с. Если систематическая погрешность определяется классом точности СИ Δ_си (или γ_си), то необходимо, чтобы доверительный интервал 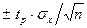был существенно меньше Δ_си.

Обычно принимают от Δ˚<Δ_с/2 до Δ˚<Δ_с/10 при Р=0,95. В случае невозможности выполнить эти соотношения необходимо коренным образом изменить методику измерения.

Методы суммирования погрешностей.

При нормировании точности технологического процесса или процесса измерения, а также при анализе действительной точности этих процессов возникает задача суммирования погрешностей, т.е. получение суммарной погрешности.

Возникает также задача разложения полученной в результате измерения суммарной погрешности на отдельные составляющие. Вторая задача является более сложной и не всегда имеет единственное, т. е. вполне определенное, решение.

Методы суммирования погрешностей различны в зависимости от вида погрешностей, т. е. в зависимости от того, являются ли погрешности величинами скалярными, векторными, постоянными или переменными, изменяющимися по экспоненциальному закону, убывающими, возрастающими или изменяющимися по периодическому закону.

Кроме того, следует различать, являются ли для данного процесса суммируемые погрешности случайными или систематическими.

Случайная погрешность

При проведении расчетов считаем погрешностью 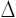x i величины x i её отклонение от среднего значения 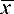. Таким образом, в дальнейшем будем полагать, что возможные для величины x i погрешности будут + 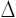x i и - 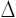x i, а диапазон изменения погрешности равен 2 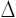x i.

Это условие учитывается во всех расчетах, так например, если в расчете участвуют величины диаметров валов d 0 = 12- 0,07, следует считать, что возможны наибольшие по абсолютной величине погрешности, т. е. отклонения от среднего размера, равные + 0,035 и - 0.035.

Согласно уравнению V lim = 6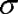 можно считать, что при нормальном распределении с вероятностью, равной 0,9973, предельная случайная погрешность измерении 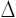lim = ± 3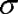 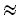± 3 s.

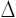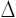Предельная погрешность для совокупности, состоящей из среднеарифметических значений, равна lim = lim/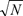, где 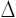lim = ± 3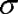 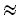± 3 s.

Из теории вероятностей известно, что дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин, поэтому

D (x 1 + x 2 + … + x n) = Dx 1 + Dx 2 + … + Dx n

Так как D = 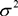, можно записать

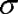(x 1 + x 2 + … + x n) = 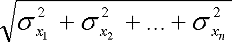или

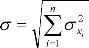(3.14)

Из полученного уравнения следует, что суммирование средних квадратических погрешностей для случайных величин, входящих в общую погрешность результата измерения, при их взаимной независимости и нормальном распределении производится квадратически.

Систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения, причем различают методическую, инструментальную и субъективную составляющие погрешности.

Субъективные систематические погрешности связаны с индивидуальными особенностями оператора. Как правило, эта погрешность возникает из-за ошибок в отсчете показаний (примерно 0.5 деления шкалы) и неопытности оператора. В основном же систематические погрешности возникают из-за методической и инструментальной составляющих.

Методическая составляющая погрешности обусловлена несовершенством метода измерения, приемами использования СИ, некорректностью расчетных формул и округления результатов.

Инструментальная составляющая возникает из-за собственной погрешности СИ, определяемой классом точности, влиянием СИ на результат и ограниченной разрешающей способности СИ.

Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие определяется следующими моментами:

• для повышения точности измерений можно выделить лимитирующие факторы, а следовательно, принять решение об усовершенствовании методики или выборе более точных СИ;

• появляется возможность определить составляющую общей погрешности, увеличивающейся со временем или под влиянием внешних факторов, а следовательно, целенаправленно осуществлять периодические поверки и аттестации;

• инструментальная составляющая может быть оценена до разработки методики, а потенциальные точностные возможности выбранного метода определит только методическая составляющая.

То есть все виды составляющих погрешности нужно анализировать и выявлять в отдельности, а затем суммировать их в зависимости от характера, что является основной задачей при разработке и аттестации методик выполнения измерений.

В ряде случаев систематическая погрешность может быть исключена за счет устранения источников погрешности до начала измерений (профилактика погрешности), а в процессе измерений — путем внесения известных поправок в результаты измерений.

· Систематические постоянные погрешности должны входить в суммарную погрешность полностью с учетом знака, т. е. должны суммироваться алгебраически.

· Систематические переменные погрешности в том случае, если определяется наибольшая величина суммарной погрешности, должны суммироваться с тем знаком, при котором абсолютная величина суммы увеличивается. Так, например, если сумма остальных слагаемых отрицательна, то в неё следует включать наибольшее по абсолютной величине отрицательное значение систематической погрешности, если она такое значение имеет или наименьшие по абсолютной величине положительные значения, если они их принимают.

Профилактика погрешности — наиболее рациональный способ ее снижения и заключается в устранении влияния, например температуры (термостатированием и термоизоляцией), магнитных полей (магнитными экранами), вибраций и т. п. Сюда же относятся регулировка, ремонт и поверка СИ.

Исключение постоянных систематических погрешностей в процессе измерений осуществляют методом сравнения (замещения, противопоставления), компенсации по знаку (предусматривают два наблюдения, чтобы в результат каждого измерения систематическая погрешность входила с разным знаком), а исключение переменных и прогрессирующих — способами симметричных наблюдений или наблюдением четное число раз через полупериоды.

Лекция 8.

Техническое регулирование.

Основные положения и цели технического регулирования

В настоящее время, производство продукции на всех стадиях жизненного цикла должно регулироваться Законом РФ "О техническом регулировании". Этот документ предусматривает разработку технических регламентов, в которых прописываются обязательные требования к выпускаемой продукции, процессам её производства, эксплуатации, хранения и утилизации. С принятием закона с июля 2003 года в России начинается процесс создания чёткой системы технического регулирования, которая в первую очередь исключает дублирование множества технических документов, разрабатываемых различными ведомствами.

Целью разработки закона является гармонизация нашей системы отношений с международной, прежде всего европейской, что даёт возможность выхода отечественных товаров на мировой рынок. Устранение барьеров в торговле обеспечивает также равные условия для российских и зарубежных производителей на российском рынке.

Федеральный закон регулирует отношения, возникающие при:

разработке,

принятии,

применении,

исполнении

обязательных требований к

продукции,

процессам производства,

эксплуатации,

хранения,

перевозки,

реализации и

утилизации,

выполнению работ или оказанию услуг;

тоже самое осуществляется и на добровольной основе; кроме того, закон регулирует отношения при оценке соответствия; устанавливает права и обязанности участников.

Выполнение работ в определенной области оценки соответствия поручается определённому физическому или юридическому лицу, для чего предоставляется аккредитация - официальное признание органом по аккредитации компетентности физического или юридического лица.

Технические регламенты и безопасность.

Технический регламент - документ, который принят международным договором Российской Федерации, ратифицированным в порядке, установленном законодательством Российской Федерации, или федеральным законом, или указом Президента Российской Федерации, или постановлением Правительства Российской Федерации и устанавливает обязательные для применения и исполнения требования к объектам технического регулирования.

Технические регламенты принимаются исключительно в целях защиты жизни или здоровья граждан, имущества физических или юридических лиц, государственного или муниципального имущества; охраны окружающей среды, жизни или здоровья животных и растений; предупреждения действий, вводящих в заблуждение приобретателей.

Содержание и применение технических регламентов строго определено. Например, должны быть установлены минимально необходимые требования, безопасности в различных сферах, при этом учитывается степень риска причинения вреда. Регламент содержит описание продукции, которое должно содержать в себе необходимые подходы и правила идентификации, т.е. тождественности характеристик продукции её существенным признакам.

Требования содержат конкретные данные, определяемые международными соглашениями. Например, документом ЕС по изделию, определено, что краска для покраски поверхности не должна содержать перечисленные химические элементы, и приведены допустимые нормы их концентрации и т.п. При разработке технических регламентов в качестве основы могут быть использованы международные и национальные стандарты.

· Технические регламенты содержат правила и методы измерений, исследований, испытаний, а также правила отбора образцов необходимых для этих целей, с учётом специфики продукции.

· Обязательные технические требования к отдельным видам продукции, процессам производства, эксплуатации, хранения, перевозки, реализации и утилизации определяются совокупностью требований общих технических регламентов и специальных технических регламентов.

· Требования общего технического регламента обязательны для применения и соблюдения в отношении любых объектов технического регулирования.

· Требованиями специального технического регламента учитываются технологические и иные особенности отдельных видов продукции, процессов производства, эксплуатации и других объектов.

Таким образом, требования общего технического регламента принимаются, например, по вопросам безопасной эксплуатации и утилизации машин и оборудования; электромагнитной совместимости; а также пожарной, экологической, ядерной, радиационной и биологической безопасности.

Специальные технические регламенты устанавливают требования только к тем отдельным видам продукции, процессам производства минимально необходимый уровень, которых не обеспечивается общими регламентами.

Разработчиком проекта технического регламента может быть любое лицо, и проект регламента должен быть доступен для ознакомления всем заинтересованным лицам, государственным органам и производителям продукции, а также для публичного обсуждения.

Наиболее значимые технические регламенты при соблюдении ряда требований к их разработке принимаются в виде федеральных законов.

Контроль (надзор) за соблюдением требований технических регламентов заключается в проверке выполнения юридическим лицом или индивидуальным предпринимателем требований технических регламентов к продукции, процессам производства, эксплуатации, хранения, перевозки, реализации и утилизации и принятие мер по результатам проверки.

Юридическое лицо или индивидуальный предприниматель, аккредитованные в установленном порядке для выполнения работ по сертификации представляют орган по сертификации.

Прямое или косвенное определение соблюдения требований, предъявляемых к объекту, есть оценка соответствия. Подтверждение соответствия заключается в документальном удостоверении соответствия продукции, процессов производства и др. требованиям технических регламентов, положениям стандартов или условиям договоров.

Поскольку любое событие совершается с определённой вероятностью, вводится понятие риск как вероятности причинения вреда жизни или здоровью граждан, имуществу физических или юридических лиц, государственному или муниципальному имуществу, окружающей среде, жизни или здоровью животных и растений с учетом тяжести этого вреда.

Понятие безопасность продукции, процессов производства, эксплуатации, хранения, перевозки, реализации и утилизации или просто безопасность соответствует состоянию, при котором отсутствует недопустимый риск, связанный с причинением вреда жизни или здоровью граждан, имуществу физических или юридических лиц, государственному или муниципальному имуществу, окружающей среде, животным, растениям.

Контроль за безопасностью продукции, осуществляемый в настоящее время нашими производителями непосредственно на производстве, для всей продукции, в том числе зарубежной, будет осуществляться, прежде всего, на рынке, как это делается в мире.

Свойства по безопасности устанавливаются государством, потому что рынок не будет заботиться о безопасности, т.к. это не выгодно рынку. Рынок заинтересован в получении прибыли. Логично предположить, что предприниматель не будет ставить очистные сооружения, он не будет проводить дополнительные исследования, чтобы доказать, что он выполнил параметры безопасности. Поэтому, государство вводит обязательные требования в интересах безопасности населения, устанавливая соответствующие технические регламенты.

Подтверждение соответствия.

Подтверждение соответствия осуществляется в целях удостоверения соответствия объектов технического регулирования техническим регламентам, стандартам, условиям договоров, а также содействия приобретателям в компетентном выборе продукции, работ и услуг.

Подтверждение соответствия должно способствовать повышению конкурентоспособности продукции, работ, услуг на российском и международном рынках, создания условий для обеспечения свободного перемещения товаров по территории Российской Федерации, а также для осуществления международного экономического, научно-технического сотрудничества и международной торговли.

Подтверждение соответствия может носить добровольный или обязательный характер.

· Обязательное подтверждение соответствия осуществляется в формах: принятия декларации о соответствии (декларирование соответствия) или обязательной сертификации.

· Добровольное подтверждение соответствия осуществляется в форме добровольной сертификации.

Ранее у нас в стране большинство наиболее значимых потребительских товаров, попадающих на рынок, должно было проходить обязательную сертификацию. Такой практики сегодня уже нет почти нигде в мире.

Лекция 9.

Сертификация и декларирование.