2014-02-10
891
Связь с индукцией магнитного поля и
Напряженность магнитного поля и ее
Рис. 7.1 отражает модель молекулярных токов в однородно намагниченном магнетике и соответствующий им поверхностный ток с линейной плотностью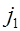 
.
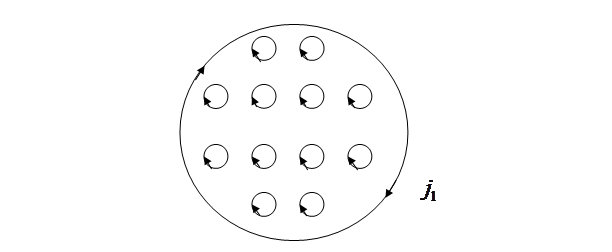
Рис. 7.1
Внутри однородного магнетика соседние участки молекулярных токов взаимно компенсируют друг друга, так что остается нескомпенсированным поверхностный ток на границе магнетика с линейной плотностью .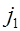
Однородный железный сердечник в форме цилиндра длиной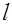 
и поперечным сечением 
поместим внутрь соленоида, по обмотке которого течет постоянный ток силой 
(см. рис. 7.2). Рис. 7.1 соответствует поперечному сечению намагниченного цилиндра.
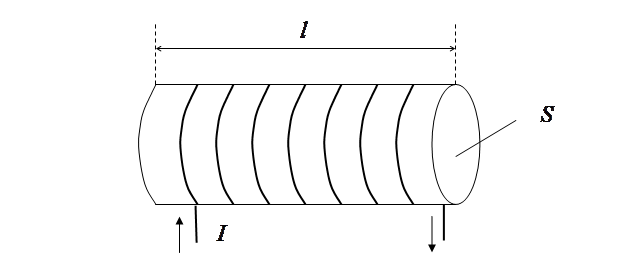
Рис. 7.2
Объем сердечника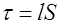 
. Магнитный момент сердечника
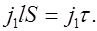
По определению намагниченности, магнитный момент сердечника можно выразить иначе как
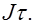
Приравнивая эти выражения, найдем
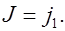
Ток обмотки соленоида создает в сердечнике внешнее магнитное поле с индукцией
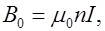
где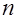 
- число витков обмотки на единицу длины соленоида, величина 
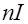имеет смысл линейной плотности тока обмотки соленоида (силы тока в расчете на единицу длины соленоида).
|
|
|
Так как магнитные моменты молекулярных токов во внешнем магнитном поле стремятся ориентироваться вдоль этого поля, то направление поверхностного тока намагничения сердечника такое же, как и у тока в обмотке. Поэтому внутреннее поле усиливает внешнее. Индукция внутреннего магнитного поля сердечника
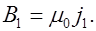
В соответствии с (7.1) индукция полного поля в сердечнике
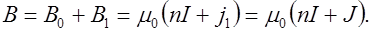(7.4)
Введем вспомогательную векторную характеристику магнитного поля в магнетике – напряженность магнитного поля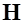 
как характеристику внешнего магнитного поля:
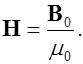(7.5)
Единица измерения напряженности магнитного поля в СИ – 1 А/м.
Так как в нашей задаче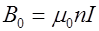 
, то напряженность магнитного поля соленоида
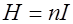. (7.6)
По опыту, в слабомагнитном (неферромагнитном) материале намагниченность пропорциональна напряженности достаточно слабого магнитного поля:
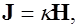(7.7)
где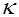 
- скалярная величина, зависящая от рода магнетика и его состояния (агрегатного состояния и температуры) и называемая магнитной восприимчивостью вещества.
С учетом (7.6) и (7.7) перепишем формулу (7.4) в векторном виде:
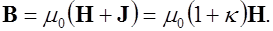(7.8)
Определение. Магнитная проницаемость вещества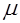 
показывает, во сколько раз магнитная индукция в катушке с сердечником больше магнитной индукции в катушке без сердечника:
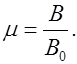
Тогда с учетом (7.5) и (7.8) найдем
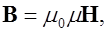(7.9)
где
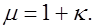(7.10)
Формулы (7.8) – (7.10) остаются справедливыми для постоянного магнитного поля в любом изотропном магнетике.
Формулу полного тока
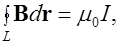(6.19)
полученную для вакуума, в магнетике перепишем для внешнего магнитного поля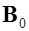 
, созданного током 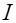, как
|
|
|
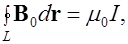(7.11)
или, с учетом (7.5) получаем формулу циркуляции напряженности магнитного поля в магнетике:
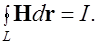(7.12)
