Возьмем два контура 1 и 2, которые расположены близко друг к другу. Пусть в контуре 1 течет переменный ток 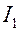 . Магнитное поле тока
. Магнитное поле тока 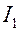 создает магнитный поток через сечение, ограниченное контуром 2. Поток пропорционален току
создает магнитный поток через сечение, ограниченное контуром 2. Поток пропорционален току 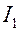 :
:
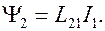 (8.9)
(8.9)
Пусть в контуре 2 течет переменный ток 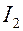 . Магнитное поле тока
. Магнитное поле тока 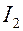 создает магнитный поток через сечение, ограниченное контуром 1. Поток пропорционален току
создает магнитный поток через сечение, ограниченное контуром 1. Поток пропорционален току 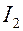 :
:
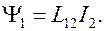 (8.10)
(8.10)
Контуры 1 и 2 называются связанными, а явление возникновения э.д.с. электромагнитной индукции в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности 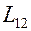 и
и 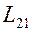 называются коэффициентами взаимной индукции. Их значения зависят от взаимного расположения контуров, их формы и размеров, а также магнитной проницаемости среды. Единица измерения коэффициентов
называются коэффициентами взаимной индукции. Их значения зависят от взаимного расположения контуров, их формы и размеров, а также магнитной проницаемости среды. Единица измерения коэффициентов 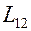 и
и 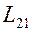 - 1 Гн.
- 1 Гн.
Пусть имеются две тороидальные однослойные катушки 1 и 2, вплотную прилегающие друг к другу (см. рис. 8.5). Внутри катушек есть неферромагнитный сердечник с магнитной проницаемостью 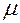 .
.
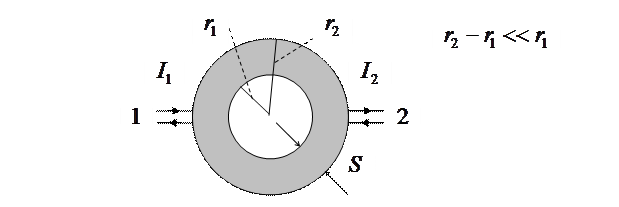

Рис. 8.5. Две обмотки с магнитной связью
В данном случае все линии индукции, создаваемые током одной катушки, проходят и через другую катушку. Обозначим 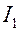 и
и 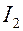 - сила тока в первой и второй катушке, соответственно,
- сила тока в первой и второй катушке, соответственно, 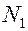 и
и 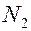 - число витков в первой и второй катушке, соответственно,
- число витков в первой и второй катушке, соответственно, 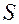 - площадь сечения катушек, и
- площадь сечения катушек, и 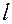 - средняя длина каждой из катушек,
- средняя длина каждой из катушек, 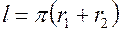 . Напряженность магнитного поля катушки 1 равна
. Напряженность магнитного поля катушки 1 равна
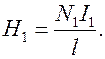
Поле 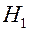 создает магнитный поток через один виток катушки 2, равный
создает магнитный поток через один виток катушки 2, равный 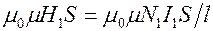 . Полный магнитный поток через катушку 2 равен
. Полный магнитный поток через катушку 2 равен
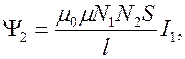
откуда коэффициент взаимной индукции
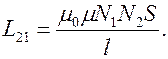
Аналогично найдем магнитный поток через катушку 1, создаваемый магнитным полем тока 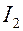 катушки 2 как
катушки 2 как
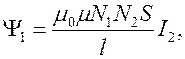
откуда коэффициент взаимной индукции
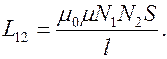
Видно, что для выбранных двух катушек коэффициенты взаимной индуктивности одинаковы:
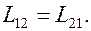 (8.11)
(8.11)
Пусть теперь внутрь катушек помещен ферромагнитный сердечник. Магнитная проницаемость такого сердечника зависит от напряженности поля: 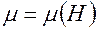 . Тогда
. Тогда
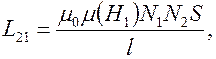
а
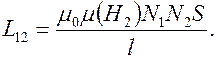
Если 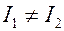 , то
, то 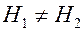 и, значит,
и, значит, 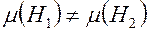 , откуда следует, что коэффициенты взаимной индукции катушек с ферромагнитным сердечником неодинаковы:
, откуда следует, что коэффициенты взаимной индукции катушек с ферромагнитным сердечником неодинаковы: 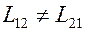 , если
, если 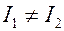 .
.
 2014-02-10
2014-02-10 929
929








