Энергия магнитного поля

Рассмотрим цепь на рис. 8.6. При замкнутом ключе 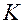через соленоид течет постоянный ток 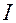. Ток соленоида порождает постоянное магнитное поле с индукцией 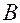. Индуктивность 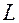соленоида без ферромагнитного сердечника не зависит от тока 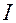, протекающего через соленоид, то есть .

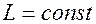Если ключ разомкнуть, то через соленоид будет течь убывающий со временем ток 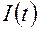, который замыкается через сопротивление 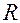. В соленоиде возникнет э.д.с. самоиндукции, равная 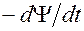, где 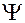- магнитный поток в соленоиде. За время 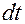по замкнутой 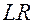- цепи будет перенесен заряд 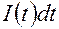. Э.д.с. самоиндукции совершит работу по переносу этого заряда, равную

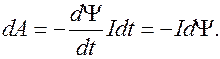
Так как 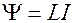, то 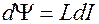. Тогда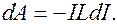

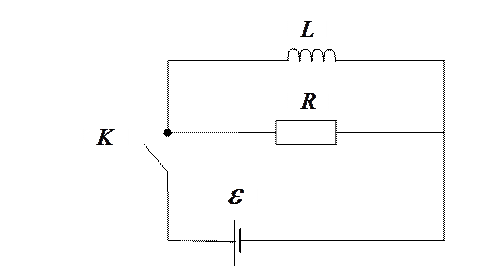
Рис. 8.6

За время убывания тока от начального значения 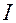до нуля э.д.с. самоиндукции совершает работу

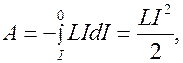(8.12)

которая идет на нагревание сопротивления 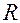и соединительных проводов.

Совершение данной работы сопровождается исчезновением магнитного поля. Других изменений, кроме нагревания сопротивления 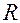и соединительных проводов, в цепи и окружающих телах не происходит. Это указывает на то, что магнитное поле является носителем энергии, за счет которой была совершена работа.

Вывод. Проводник с индуктивностью 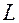, по которому течет ток силы 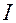, обладает энергией

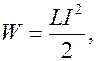(8.13)

которая локализована в магнитном поле, созданном током.

Величина 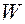из (8.13) называется собственной энергией тока .

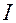Если ключ первоначально был разомкнут, а затем замкнут, то источник э.д.с. 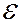совершает работу по установлению тока от начального значения, равного нулю, до стационарного значения 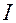. Часть этой работы, равная 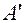, идет на создание магнитного поля соленоида. Эта часть работы совершается против э.д.с. самоиндукции и равна

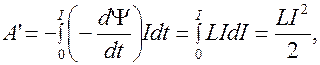
что совпадает с (8.12).

Выразим энергию магнитного поля через характеристики самого поля. В случае соленоида имеем:

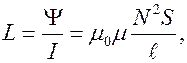(8.7)

откуда

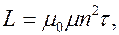(8.14)

где 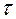- объем соленоида, .

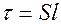Кроме того,

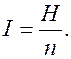(8.15)

Подставим (8.14) и (8.15) в (8.13), найдем

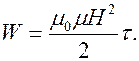(8.16)

Внутри идеального соленоида энергия магнитного поля распределена равномерно, поэтому плотность энергии магнитного поля

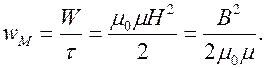(8.17)

Выражение (8.17) можно переписать и в векторном виде:

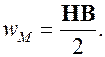(8.18)

Из теории электромагнетизма следует, что выражения (8.17) и (8.18) остаются справедливыми для любого изотропного магнитного поля, как однородного, так и неоднородного.

Энергия магнитного поля в объеме 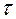равна

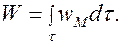(8.19)

Пусть имеются две тороидальные однослойные катушки 1 и 2, вплотную прилегающие друг к другу (см. рис. 8.5). Внутри катушек есть неферромагнитный сердечник с магнитной проницаемостью .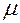

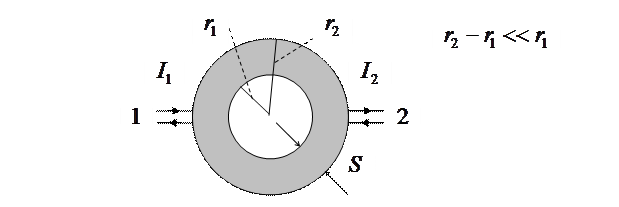
Рис. 8.5. Две обмотки с магнитной связью

Напряженность суммарного магнитного поля внутри катушек

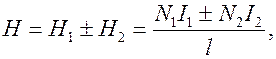
где выбор знака зависит от того, совпадают или противоположны направления токов в катушках.

Энергия магнитного поля в объеме катушек

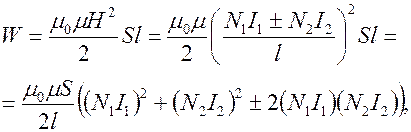
откуда энергия магнитного поля катушек с магнитной связью равна

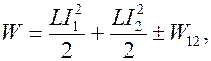(8.20)

где величина

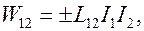(8.21)

называется энергией взаимной связи двух токов.

Вывод: Энергия магнитного поля катушек с магнитной связью отличается от суммы собственных энергий токов катушек на величину энергии взаимной связи двух токов.

Причина этого отличия – в нелинейной зависимости энергии магнитного поля от напряженности магнитного поля.