Автоматизация измерения частоты и периода. Временные диаграммы

Измерение периода периодического сигнала – это новый случай общей задачи измерения интервала времени.

По отношению к периоду периодического сигнала моменты положения опорного и интервального импульсов на оси времени – это моменты двух соседних переходов исследуемого сигнала через нулевой уровень с производной одинакового знака (например, положительного) (также его можно видеть из рисунка 4.12 как пресечение оси времени снизу вверх – нулевой уровень в производной одинакового знака)

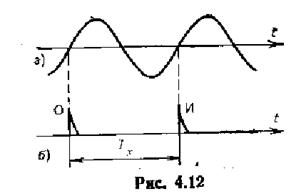
Не следует делать общие заключения, что для измерения периода синусоидального сигнала или длительности прямоугольного импульса обязательно требуется преобразование этих сигналов в два коротких импульса.

Его можно увидеть принцип измерения синусоидального сигнала методом дискретного счёта.

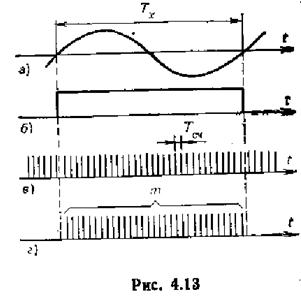
Принцип измерения синусоидального сигнала методом дискретного счета можно увидеть на том рисунке 4.13

Исследуемый сигнал (4.13а) преобразуется в прямоугольный импульс (4.13б), который вырезает из периодической последовательности счетных импульсов (4.13в) участок содержащий m импульсов (4.13г). Т.к. период их следования Т_сч, значение измеряемого периода Т_х есть:

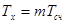
Т.е. структурная схема устройства для измерения периода из полученных результатов вытекает на рис 4.14

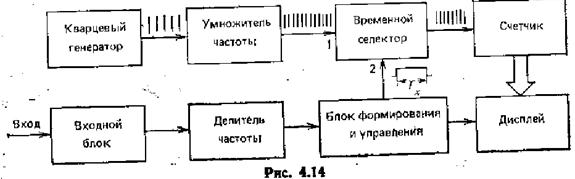
На 4.14 мы висим, что это есть «общая схема цифрового частотомера во время измерения периода».

Из исследуемого сигнала х, период Тх, который необходимо измерить, во входном блоке формируется периодическая поседовательность коротких импульсов с периодом следования Т_х.

В блоке формирования и управления из них формруется прямоугольный стобирующий импульс длительностью Т_х (есть на 4.13).

Если включить делитель частоты, с коэффициентом деления q, то время следования импульсов на его выходе получается равным q*Tx. Такую же длительность имеет страбирующий импульс.

Он подводится к входу 2 временного селектора на вход 1 которого подаются импульсы кварцевого генератора, являющиеся счетными импульсами. Частота их следования есть fкварцевания (fкв)

Таким образом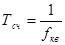

При этом измеряемый период связан с показанием счетчика m и частотой кварцевой генератора f_{к в} с соотношением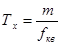

Составляющие погрешность измерения периода периодического сигнала принципиально те же, что были рассмотрены при анализе измерений интервалов времени заданного опорным и интервальным импульсами.

Максимальная абсолютная погрешность дискретности есть дельта тэ равная плюс минус дельта тэ счетчика:

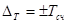
А соотвующая относительная погрешность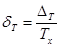

Из этого же выражения вытекает что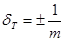

Когда измеряется q периодов, то относительная погреш дискретности уменьшается тоже в q раз.

При измерении периода значительный вклад в общую погрешность может внести составляющая, обусловленная действием шумовой помехи при формировании страбирующего импульса, т.е. погрешность запуска триггера.

При таких расчетах пользуются среднеквадратическим значением относительной погрешности δ:

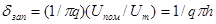, где q – число одновременно измеряемых периодов сигнала; U_пом – средневадратическое значение напряжения помехи; U_m – амплитуда напряжения сигнала, 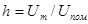- отношение сигнал-помеха.

Например, при отношении сигнао-помеха 40дБ (h=100) и q=1 относительная среднеквадратичная погрешность 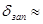0,3 %.

Если при таком же отношении измерять интервал времени, равный 100 периодов сигнала, то 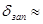0,003%

Предел относительно допускаемой погрешнсоти цифрового измерителя периода, выражается в процентах по отношению к периоду Тх формулой

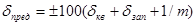
При этом в этой формуле 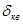- общая погрешность меры (кварцевого генератора)