Энергия заряженного конденсатора
Обозначим 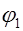 - потенциал обкладки конденсатора с зарядом
- потенциал обкладки конденсатора с зарядом 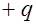 ,
, 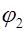 - потенциал обкладки конденсатора с зарядом
- потенциал обкладки конденсатора с зарядом 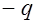 . Энергия такой системы
. Энергия такой системы
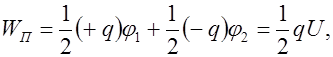
где 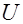 - напряжение между обкладками конденсатора,
- напряжение между обкладками конденсатора, 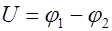 .
.
Емкость конденсатора 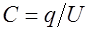 , тогда его энергия
, тогда его энергия
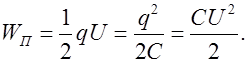
Выразим энергию заряженного конденсатора через параметры электрического поля в зазоре между его обкладками. Для определенности возьмем плоский конденсатор, емкость которого
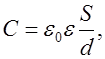
где 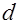 - расстояние между пластинами конденсатора,
- расстояние между пластинами конденсатора, 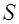 - площадь каждой обкладки конденсатора.
- площадь каждой обкладки конденсатора.
Имеем:
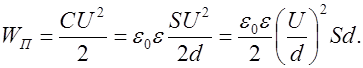
Так как объем конденсатора 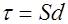 , а напряженность поля в нем
, а напряженность поля в нем 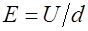 , то
, то
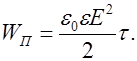
Постоянные поля и их источники – неподвижные заряды, не могут существовать отдельно друг от друга. Меняющиеся во времени электромагнитные поля могут существовать и в отсутствие электрических зарядов. Распространяясь в пространстве, такие поля образуют электромагнитные волны. Это свидетельствует в пользу вывода о том, что энергия заряженного конденсатора – это энергия электрического поля между его обкладками.
В плоском конденсаторе электрическое поле однородно, что позволяет выразить плотность энергии электрического поля в расчете на единицу объема:
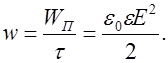
Если поле – неоднородное, то плотность энергии может изменяться от точки к точке: 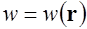 , где
, где 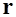 - радиус-вектор точки наблюдения. С учетом выражений для электрической индукции
- радиус-вектор точки наблюдения. С учетом выражений для электрической индукции 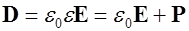 , выражение для плотности энергии можно обобщить как
, выражение для плотности энергии можно обобщить как
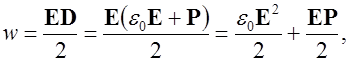
где первое слагаемое совпадает с плотностью энергии электрического поля в вакууме, а второе слагаемое представляет собой энергию, которая затрачивается на поляризацию диэлектрика.
Энергия электрического поля в объеме 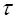 равна
равна
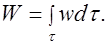
 2014-02-10
2014-02-10 344
344







