Оптическая сила сферической границы

Матрица трансляции. Матрица преломления на сферической границе.

Матричная оптика. Опорная плоскость. Координаты луча.

Плоскость перпендикулярную оптической оси назовем опорной плоскостью.

Рассмотрим две опорные плоскости. Каждый луч в первой опорной плоскости будем характеризовать двумя координатами: расстояние 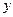от оптической оси и произведени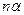е , где 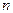— показатель преломления в первой опорной плоскости, 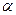— угол между лучом и оптической осью. Из двух координат луча можно составить вектор 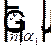в некотором абстрактном пространстве. Здесь индекс 1 относится к первой опорной плоскости. Координаты луча во второй опорной плоскости, если между плоскостями однородная среда с показателем преломления 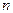, можно найти из системы 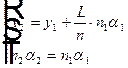, где 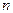, , 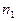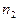— один и тот же показатель преломления среды между опорными плоскостями, 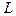— расстояние между опорными плоскостями.

Тогда координаты луча во второй опорной плоскости можно выразить через координаты луча в первой опорной плоскости с помощью некоторой матрицы 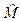: 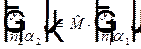, где

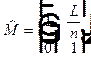называется матрицей трансляции.

Для преломления на сферической границе 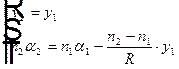, где второе уравнение было получено в предыдущем вопросе. Тогда

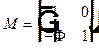— матрица преломления на сферической границе, где

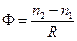— оптическая сила сферической границы.

Заметим, что если рассмотреть три опорные плоскости, то 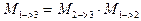, так как каждая часть равенства 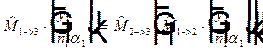равна вектору .

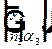Следовательно, перемножением матриц трансляции и преломления на сферической границе можно найти матрицу оптической системы любой сложности. Порядок перемножения матриц обратный по отношению к порядку, в котором луч встречает элементы оптической схемы.