Факультативно. Величина лучевой и фазовой скорости в простейшем случае

Простейший случай — это когда направление вектора 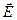световой волны совпадает с одной из главных диэлектрических осей кристалла (пусть с осью x). В главных диэлектрических осях связь векторов 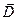и 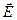выглядит достаточно просто 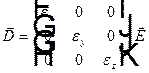. Откуда получаем 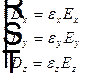. Если вектор 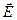направлен вдоль оси x, то 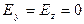, откуда вектор 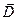тоже имеет только составляющую 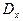. Следовательно, в рассматриваемом случае векторы 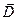и 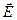сонаправлены и кристаллическая среда ведет себя аналогично изотропной среды. Величина лучевой скорости в кристалле всегда зависит только от направления вектора 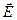, а не от направления света. Тогда 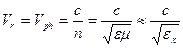— лучевая и фазовая скорости совпадают по величине и направлению (угол между лучевой и фазовой скоростями равен углу между векторам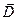и и 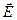, который равен нулю).

Фазовая пластинка.

Рассмотрим случай, когда свет распространяется вдоль одной из главных диэлектрических осей кристалла. Пусть 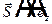. Поскольку 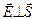, вектор 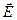лежит в плоскости x,y. Разложим вектор 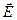на составляющие вдоль осей x и y. Каждая из двух составляющих будет иметь вектор 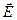, направленный вдоль главной диэлектрической оси кристалла. Следовательно, каждая из двух составляющих поля будет иметь свою лучевую скорость, совпадающую с фазовой скоростью, 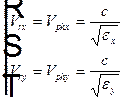. Для этих двух лучей показатели преломления не равны 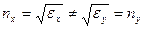— двулучепреломление.

Фазовая пластинка — плоско параллельная кристаллическая пластинка, у которой две главные диэлектрические оси с различающимися диэлектрическими проницаемостями лежат в плоскости пластины.

Пластинк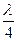и и .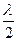

Фазовая пластинка с оптической разностью хода 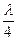для двух линейных поляризаций называется пластинкой .

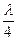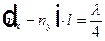
Для пластинки 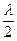разность хода — 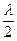и соответственно .

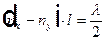Лучевой эллипсоид. Определение поляризации и лучевой скорости лучей по лучевому эллипсоиду (без доказательства).

Направим оси координат вдоль главных диэлектрических осей кристалла. Рассмотрим поверхность так называемого лучевого эллипсоида, уравнение которого 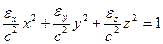. Главные полуоси эллипсоида имеют длины 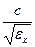, , 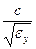, 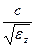равные лучевым скоростям, когда вектор 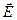направлен вдоль соответствующих осей.

Алгоритм нахождения поляризаций двух световых волн для заданного направления луча 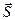следующий. 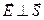, поэтому векторы 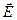обеих волн лежат в плоскости перпендикулярной лучу. Рассмотрим сечение эллипсоида плоскостью перпендикулярной лучу 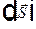, проходящей через центр эллипсоида. Сечение эллипсоида — эллипс. Оси эллипса — направления вектора 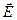двух лучей. Длина полуосей эллипса — лучевые скорости двух лучей.