2014-02-10
687
Формула тонкой линзы. Сопряженные плоскости.
Рассмотрим две опорные плоскости на расстояниях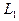 
и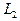 
с двух сторон тонкой линзы с оптической силой 
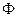. Матрица перехода от первой ко второй опорной плоскости 
= 
.
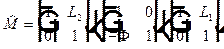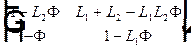В соответствии с этой матрицей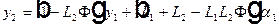 
. Рассмотрим это уравнение применительно к точечному предмету в первой опорной плоскости и его изображению во второй опорной плоскости. Плоскости предмета и изображения называются сопряженными плоскостями. Тогда пучок лучей, выходящих из точки 
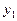под любыми углами 
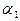должен собраться в точку 
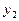. Если равенство сохраняется при любом 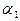, то коэффициент при 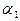должен быть равен нулю 
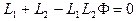. Откуда 
.
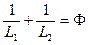Если среды слева и справа от тонкой линзы имеют показатели преломления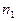 
и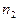 
, то во всех формулах этого вывода нужно заменить 
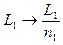и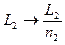 
. Тогда 
.
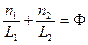Учтем теперь правило знаков в параксиальной оптике. Если предмет слева от линзы и его x координата равна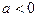 
, а изображение справа от линзы и его x координата равна 
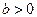, то
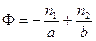— формула тонкой линзы.
Пусть теперь на линзу падает параллельный пучок лучей (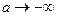
), тогда точка, в которой он собирается, называется фокусом линзы (задним фокусом). Координата фокуса относительно линзы называется фокусным расстоянием 
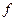. Тогда
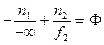, откуда 
.
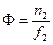Если свет выходит из некоторой точки на оптической оси, и после линзы свет идет в виде параллельного пучка лучей, то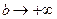 
и свет выходит из переднего фокуса, а его координата относительно линзы равна переднему фокусному расстоянию 
.
.
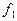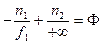Оба фокусных расстояния связаны с оптической силой линзы соотношением
.
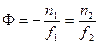Фокальная плоскость — плоскость перпендикулярная оптической оси и проходящая через фокус.
