Статистическая гипотеза есть некоторое предположение относительно свойств генеральной совокупности, из которой извлекается выборка. Критерий статистической гипотезы— это правило, позволяющее принять или отвергнуть данную гипотезу на основании выборки. При построении такого правила используются определенные функций результатов наблюдений g(х1,х2,...,хN), называемые статистиками для проверки гипотез. Все возможные значения подобных статистик делятся на две части: область принятия гипотезы и критическую область. Проверка гипотезы сводится к выяснению того, попадает или нет конкретное значение статистики, вычисленное по выборке, в критическую область: если нет—гипотеза принимается, как не противоречащая результатам наблюдения, если да—гипотеза отвергается. При этом всегда возможно совершить ошибку; различные типы возможных ошибок указаны в табл. 2.2.
Таблица 2.2
| Гипотеза | Объективно верна | Объективно неверна |
| Принимается | Правильное решение | Ошибка II рода |
| Отвергается | Ошибка I рода | Правильное решение |
Вероятность совершить ошибку I рода называется уровнем значимости критерия и обозначается q. Обычно уровень значимости выбирают равным 0,01; 0,1; 0,05 (последнее значение— наиболее часто).
|
|
|
Критерии значимости — это критерии, с помощью которых проверяют гипотезы об абсолютных значениях параметров или о соотношениях между ними для генеральных совокупностей с известной (с точностью до параметров) функцией распределения вероятностей.
Для пояснения идеи построения критериев значимости предположим, что некоторая оценка 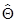 , используемая затем в качестве статистики g, вычислена по выборке объема N. Пусть имеются причины считать, что истинное значение оцениваемого параметра
, используемая затем в качестве статистики g, вычислена по выборке объема N. Пусть имеются причины считать, что истинное значение оцениваемого параметра 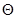 , т. е. его значение в генеральной совокупности, равно
, т. е. его значение в генеральной совокупности, равно 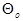 . Это проверяемое предположение часто называют нулевой гипотезой Но и пишут Но:
. Это проверяемое предположение часто называют нулевой гипотезой Но и пишут Но: 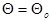 .
.
Даже если нулевая гипотеза справедлива, то выборочное значение 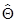 обычно не совпадает точно с
обычно не совпадает точно с 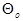 , поскольку оно является всего лишь одним из конкретных значений случайной величины
, поскольку оно является всего лишь одним из конкретных значений случайной величины 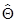 , порожденной всевозможными выборками объема N. Спрашивается: насколько сильно
, порожденной всевозможными выборками объема N. Спрашивается: насколько сильно 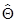 должно отличаться от
должно отличаться от 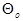 , чтобы в достаточной мере обоснованно можно было отвергнуть нулевую гипотезу? Если известна функция плотности вероятности оценки f(
, чтобы в достаточной мере обоснованно можно было отвергнуть нулевую гипотезу? Если известна функция плотности вероятности оценки f(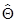 ), построенная теоретически в предположении справедливости нулевой гипотезы, то с её помощью несложно найти такую зону, вероятность случайных попаданий в которую (когда Но верна) мала (равна малому значению q). Эта зона и может использоваться в качестве критической области критерия.
), построенная теоретически в предположении справедливости нулевой гипотезы, то с её помощью несложно найти такую зону, вероятность случайных попаданий в которую (когда Но верна) мала (равна малому значению q). Эта зона и может использоваться в качестве критической области критерия.
Вид критической области полностью определяется характером альтернативной гипотезы h1, т. е. гипотезы, противопоставляемой нулевой, той гипотезы, в пользу которой склоняется исследователь, отвергая проверяемую нулевую гипотезу.
|
|
|
Если нулевой гипотезе Но: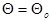 противопоставляется альтернативная гипотеза
противопоставляется альтернативная гипотеза 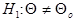 , то критерий для проверки Но носит название двустороннего, а его критическая область состоит из двух частей. Если же альтернативная гипотеза формулируется в виде
, то критерий для проверки Но носит название двустороннего, а его критическая область состоит из двух частей. Если же альтернативная гипотеза формулируется в виде 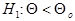 или
или 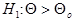 , то соответствующие критерии называются односторонними и их критические области содержат всего одну часть.
, то соответствующие критерии называются односторонними и их критические области содержат всего одну часть.
В табл. 2.3 приведены некоторые стандартные критерии, позволяющие проверять гипотезы о значениях математических ожиданий и дисперсий нормальных генеральных совокупностей при независимых наблюдениях в выборке.
Таблица 2.3
| № | Проверяемая гипотеза Но и альтернативная гипотеза Н1 | Информация о параметрах распределения | Статистика g и ее обозначение для каждого критерия | Распределение статистики g при справедливой гипотезе Но | Критическая область | ||
| Но:mx=mo H1:mx¹mo | |||||||
| Ho:mx=mo H1:mx<mo | 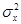 неизвестно неизвестно | 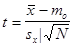 | t-распределение с n=N-1 степенями свободы | ||||
| Ho:mx=mo H1:mx>mo | |||||||
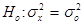 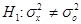 | |||||||
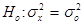 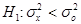 | mx неизвестно | 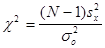 | c2- распределение с n=N-1 степенями свободы | ||||
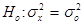 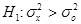 | |||||||
| 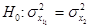 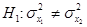 | 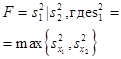 | |||||
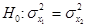 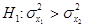 | 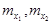 неизвестны неизвестны | 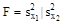 | |||||
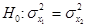 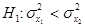 | 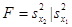 |
Критерием согласия называется критерий гипотезы о том, что генеральная совокупность имеет распределение предполагаемого типа (например, нормальное распределение). Существуют несколько критериев согласия: критерий согласия Пирсона, Колмогорова, и др. Процедура проверки согласия опытного и теоретического распределения случайной величины состоит в построении эмпирического распределения, полученного по независимым измерениям, случайной величины X, определении некоторой функции накопленных частот и сравнении ее с теоретической при заданном уровне значимости. Среди различных критериев согласия наиболее употребителен универсальный критерий согласия c2 (Пирсона).
Критерий согласия Пирсона c2. Сущность метода идентификации эмпирического закона с использованием критерия c2 достоит в том, что в качестве меры расхождения между, эмпирической и предполагаемой теоретической плотностями распределения используется статистика:
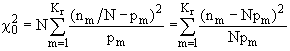
асимптотически подчиненная распределению c2. Здесь nm — число наблюдений в m-ом разряде, m=[1;Kr]; N — число опытов (объем выборки); pm — вероятность попадания случайной величины X в m-й разряд, вычисленный для предполагаемого теоретического закона распределения f(x). Вероятность попадания непрерывной случайной величины в интервал [x1, x2] вычисляется в общем случае из соотношения:
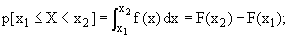
где F(x) — функция распределения вероятностей или интегральная функция распределения.
Закон распределения 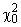 при неограниченном увеличении N зависит только от числа разрядов Kr и стремится к распределению c2 со степенями свободы
при неограниченном увеличении N зависит только от числа разрядов Kr и стремится к распределению c2 со степенями свободы 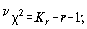 , где r — число параметров предполагаемого теоретического закона распределения, найденных по данной выборке (для нормального закона распределения r=2). Таким образом, вычисленную для данной выборки N величину
, где r — число параметров предполагаемого теоретического закона распределения, найденных по данной выборке (для нормального закона распределения r=2). Таким образом, вычисленную для данной выборки N величину 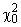 сравнивают с критической точкой, взятой из таблиц теоретического распределения, по заданному уровню значимости
сравнивают с критической точкой, взятой из таблиц теоретического распределения, по заданному уровню значимости 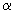 и числу степеней свободы
и числу степеней свободы 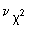 .
.
Если 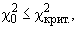 , отклонение теоретического и эмпирического закона распределения считается незначимым, то проверяемая статистическая гипотеза верна. В противном случае гипотеза отвергается.
, отклонение теоретического и эмпирического закона распределения считается незначимым, то проверяемая статистическая гипотеза верна. В противном случае гипотеза отвергается.
 2014-02-10
2014-02-10 5626
5626