Точечные оценки параметров не дают информации о степени близости оценки 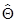 к соответствующему теоретическому параметру
к соответствующему теоретическому параметру 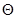 . Поэтому более информативный способ оценивания неизвестных параметров состоит не в определении единичного точечного значения, а в построении интервала, в котором с заданной степенью достоверности окажется оцениваемый параметр, т. е. в построении так называемой интервальной оценки параметра
. Поэтому более информативный способ оценивания неизвестных параметров состоит не в определении единичного точечного значения, а в построении интервала, в котором с заданной степенью достоверности окажется оцениваемый параметр, т. е. в построении так называемой интервальной оценки параметра 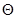 .
.
Интервальной оценкой параметра в называется интервал, границы которого 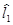 и
и 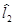
 являются функциями выборочных значений x1,x2,...xN и который с заданной вероятностью p накрывает оцениваемый параметр
являются функциями выборочных значений x1,x2,...xN и который с заданной вероятностью p накрывает оцениваемый параметр 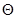 :
:
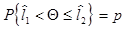 . (2.4)
. (2.4)
Интервал (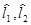 ) называется доверительным, его границы
) называется доверительным, его границы 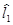 и
и 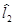 являющиеся случайными величинами,—соответственно нижним и верхним доверительными пределами, вероятность р— доверительной вероятностью, а величина q = 1— р — уровнем значимости, используемым при построении доверительного интервала. Любая интервальная оценка может быть охарактеризована совокупностью двух чисел: шириной доверительного интервала
являющиеся случайными величинами,—соответственно нижним и верхним доверительными пределами, вероятность р— доверительной вероятностью, а величина q = 1— р — уровнем значимости, используемым при построении доверительного интервала. Любая интервальная оценка может быть охарактеризована совокупностью двух чисел: шириной доверительного интервала 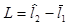 являющейся мерой точности оценивания параметра
являющейся мерой точности оценивания параметра 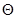 , и доверительной вероятностью р, характеризующей степень достоверности (надежности) результатов. Практически чаще всего используется значение р =0,95, несколько реже р=0,9 и р=0,99 и совсем редко р =0,8 и р =0,999.
, и доверительной вероятностью р, характеризующей степень достоверности (надежности) результатов. Практически чаще всего используется значение р =0,95, несколько реже р=0,9 и р=0,99 и совсем редко р =0,8 и р =0,999.
Общая процедура получения интервальной оценки состоит в следующем:
1. Записывают определенное вероятностное утверждение вида
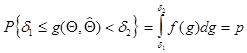 , (2.5)
, (2.5)
где f (g) — функция плотности вероятности случайной величины g. При этом значения d1 и d2 определяют обычно с учетом дополнительных условий:
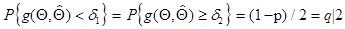 (2.6)
(2.6)
2. Аргумент выражения (2.5) преобразуют так, чтобы в окончательном виде оцениваемый параметр оказался заключенным между величинами, определяемыми по выборке. Это и будут границы доверительного интервала (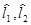 ). Функцию g(
). Функцию g( ) выбирают таким образом, чтобы она допускала подобное преобразование и имела известную (лучше табулированную) функцию плотности вероятности f{g). Последнее обстоятельство существенно упрощает определение значений d1 и d2.
) выбирают таким образом, чтобы она допускала подобное преобразование и имела известную (лучше табулированную) функцию плотности вероятности f{g). Последнее обстоятельство существенно упрощает определение значений d1 и d2.
В табл. 2.1 указаны сведения, необходимые для построения доверительных интервалов для среднего значения mx, когда 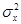 неизвестна, для дисперсии
неизвестна, для дисперсии 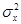 и среднего квадратического отклонения sx. Предполагается, что Х — нормальная случайная величина, а наблюдения независимы. Соответствующие формулы имеют следующий вид:
и среднего квадратического отклонения sx. Предполагается, что Х — нормальная случайная величина, а наблюдения независимы. Соответствующие формулы имеют следующий вид:
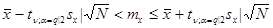

 , (2.9)
, (2.9)
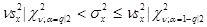
 , (2.10)
, (2.10)
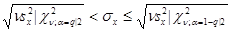
 . (2.11)
. (2.11)
В этих формулах v = N—1, q=1—p, где р—доверительная вероятность.
Таблица 2.1
Параметр 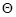
| Информация о параметрах распределения | Функция g( ) )
| Распределение f(g) | Формула для нахождения доверительного интервала |
| mx | 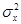 неизвестна неизвестна
| 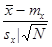 
| t- распределение | (2.9) |
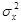
| mx неизвестно |  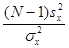 
| c2- распределение | (2.10) |
| sх | -/- | -/- | -/- | (2.11) |
 2014-02-10
2014-02-10 1058
1058








