Контрольные вопросы и задачи
Литература
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Каплянский А.Е. и др. Теоретические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. –М.: Высш. шк., 1972. –448 с.
- В чем заключается сущность метода кусочно-линейной аппроксимации?
- На чем основан метод гармонического баланса?
- Сформулируйте основные этапы расчета нелинейной цепи методом гармонического баланса.
- В чем состоит сущность метода расчета по первым гармоническим?
- Как определяется характеристика нелинейного элемента для первых гармоник?
- Резистивная нагрузка подключена к источнику синусоидального напряжения через последовательно включенный с ней диод. Считая ВАХ диода идеальной, определить коэффициент мощности. Обоснуйте физически полученный результат.
Ответ: 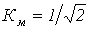 .
.
- Последовательно соединенные линейный конденсатор с
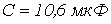 и нелинейная катушка, вебер-амперная характеристика которой аппроксимирована выражением
и нелинейная катушка, вебер-амперная характеристика которой аппроксимирована выражением 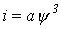 , где
, где 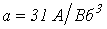 , питаются от источника синусоидального напряжения
, питаются от источника синусоидального напряжения 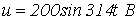 . Ограничившись рассмотрением первой и третьей гармонических, определить потокосцепление.
. Ограничившись рассмотрением первой и третьей гармонических, определить потокосцепление.
Ответ: 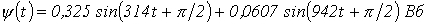
| Лекция N 37. Метод эквивалентных синусоид (метод расчета по действующим значениям). |
Сущность метода эквивалентных синусоид была изложена в лекции №35 при рассмотрении его графической реализации. При аналитическом варианте применения метода отсутствует основной этап графических построений, в частности векторных диаграмм, который заменяется соответствующими вычислениями с использованием аналитических соотношений для комплексов эквивалентных синусоидальных величин. Графический вариант применения метода эквивалентных синусоид характеризуется, в первую очередь для относительно простых схем, большей наглядностью. В то же время при аналитическом подходе повышается точность расчетов за счет устранения погрешностей, связанных с графическими построениями.
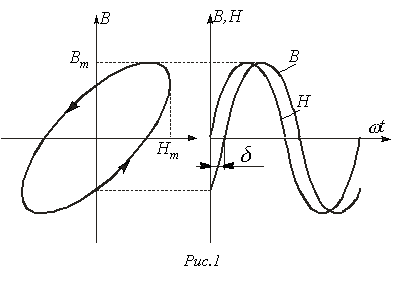
Переход к эквивалентным синусоидам соответствует замене реальных петель гистерезиса
где
При переменных токах потери в стали сердечника определяются не только гистерезисом, но и вихревыми токами, вызываемыми переменным потоком. Таким образом, динамическая петля гистерезиса шире статической и отличается от последней по форме. Отметим, что для уменьшения потерь от вихревых токов сердечник набирают из изолированных тонких листов (при частоте При пренебрежении неравномерностью распределения магнитной индукции по сечению мощность потерь от вихревых токов определяется соотношением
где В свою очередь мощность потерь от гистерезиса
где n=1,8…2,2 (часто в первом приближении принимается n=2); Полные потери в стали
Для определения параметров эквивалентной синусоиды тока: его действующего значения и угла потерь (фазового сдвига относительно магнитного потока) - удобно пользоваться соотношением для мощности потерь в стали
и намагничивающей мощности
где Переход к эквивалентным синусоидам и соответственно к эквивалентному эллипсу, заменяющему реальную кривую зависимости
где и комплексное магнитное сопротивление
являющееся аналогом магнитному сопротивлению
Различают параллельную и последовательную схемы замещения катушки с ферромагнитным сердечником. Эти схемы, а также соответствующие им соотношения и векторные диаграммы приведены в табл. 1. Таблица 1. Схемы замещения, уравнения и векторные диаграммы для катушки c ферромагнитным сердечником
Примечание. 1. Если сердечник содержит воздушный зазор величиной
2. При пренебрежении активным сопротивлением обмотки и потоком рассеяния связь между эквивалентным электрическим сопротивлением
или
 Сейчас читают про:
|
 2014-02-10
2014-02-10 710
710

 Переход к эквивалентным синусоидам в сочетании с символическим методом позволяет составлять эквивалентные схемы замещения с эквивалентными параметрами
Переход к эквивалентным синусоидам в сочетании с символическим методом позволяет составлять эквивалентные схемы замещения с эквивалентными параметрами 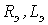 и
и 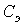 . Трудности анализа и расчета заключаются в том, что значения этих параметров зависят от искомых напряжений, токов и потоков, т. е. заранее не известны.
. Трудности анализа и расчета заключаются в том, что значения этих параметров зависят от искомых напряжений, токов и потоков, т. е. заранее не известны.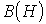
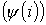 или
или 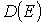
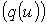 эквивалентными эллипсами. На рис. 1 представлен эквивалентный эллипс, заменяющий реальную кривую
эквивалентными эллипсами. На рис. 1 представлен эквивалентный эллипс, заменяющий реальную кривую 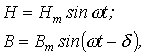
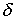 -угол потерь, определяющий мощность потерь в единице объема ферромагнетика за один цикл перемагничивания
-угол потерь, определяющий мощность потерь в единице объема ферромагнетика за один цикл перемагничивания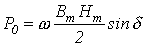 .
.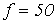 Гц их толщина
Гц их толщина 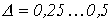 мм), выполненных из сталей со специальными присадками, снижающими проводимость.
мм), выполненных из сталей со специальными присадками, снижающими проводимость.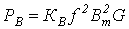 ,
,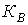 - эмпирический коэффициент, определяемый сортом стали и размером листов; G – масса сердечника.
- эмпирический коэффициент, определяемый сортом стали и размером листов; G – масса сердечника.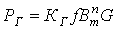 ,
,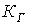 - эмпирический коэффициент, зависящий от сорта стали.
- эмпирический коэффициент, зависящий от сорта стали.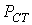 , помимо указанных, определяются также дополнительными
, помимо указанных, определяются также дополнительными 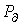 , связанными с магнитной вязкостью материала, т.е.
, связанными с магнитной вязкостью материала, т.е.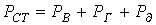 .
.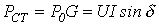
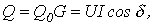
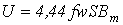 – напряжение, приложенное к нелинейной катушке индуктивности с числом витков
– напряжение, приложенное к нелинейной катушке индуктивности с числом витков 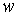 и площадью сечения сердечника
и площадью сечения сердечника 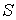 ;
; 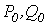 -соответственно удельные (на единицу массы сердечника) потери в стали и намагничивающая мощность. Значения
-соответственно удельные (на единицу массы сердечника) потери в стали и намагничивающая мощность. Значения 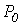 и
и  берутся из экспериментальных характеристик
берутся из экспериментальных характеристик 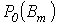 и
и 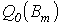 , выражающих зависимости этих величин от амплитуды индукции (см. в качестве примера кривые на рис. 2) в режиме синусоидальной индукции.
, выражающих зависимости этих величин от амплитуды индукции (см. в качестве примера кривые на рис. 2) в режиме синусоидальной индукции.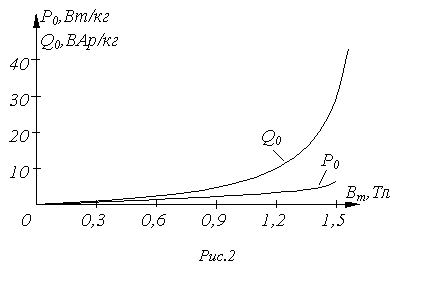
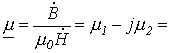
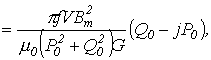
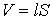 - объем стали сердечника длиной
- объем стали сердечника длиной 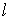 и сечением
и сечением 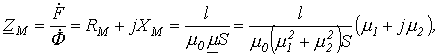
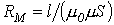 в нелинейных цепях при постоянных магнитных потоках.
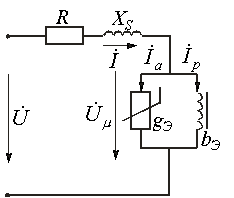
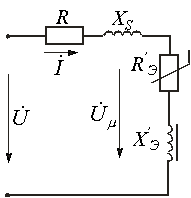
в нелинейных цепях при постоянных магнитных потоках.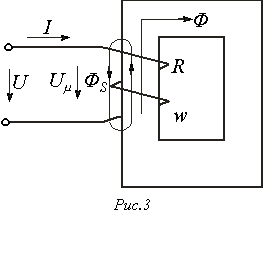 Нелинейная катушка индуктивности изображена на рис. 3. Здесь R-активное сопротивление обмотки с числом витков w; Ф-основной поток, замыкающийся по сердечнику;
Нелинейная катушка индуктивности изображена на рис. 3. Здесь R-активное сопротивление обмотки с числом витков w; Ф-основной поток, замыкающийся по сердечнику; 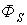 -поток рассеяния, которому соответствует индуктивность рассеяния
-поток рассеяния, которому соответствует индуктивность рассеяния 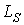 и индуктивное сопротивление рассеяния
и индуктивное сопротивление рассеяния  .
.
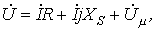 где
где 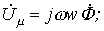
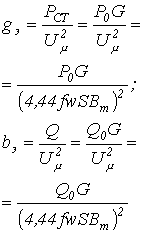
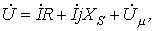 где
где 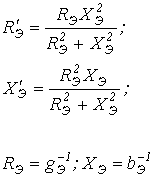
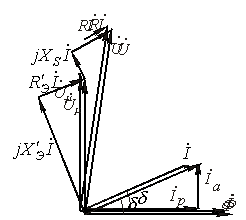
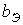 , включается дополнительная линейная катушка индуктивности с сопротивлением
, включается дополнительная линейная катушка индуктивности с сопротивлением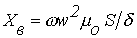
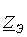 катушки и комплексным магнитным сопротивлением
катушки и комплексным магнитным сопротивлением 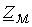 сердечника определяется соотношением
сердечника определяется соотношением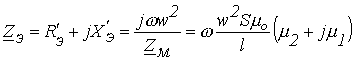
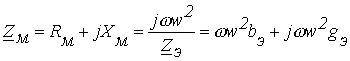 .
.





