1) Так как балансовая прибыль зависит от объема реализованной продукции, то в качестве факторного признака (x) будет выступать объем реализованной продукции, а в качестве результативного (y) – балансовая прибыль.
Уравнение линейной регрессии найдем по формуле:
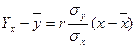 ,
,
Рассчитаем необходимые суммы в таблице 8.2.
Таблица 8.2
| x | y | 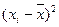
| 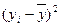
| 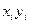
| |
| 1,2 | 537,397 | 6,205 | |||
| 1,8 | 330,579 | 3,576 | |||
| 84,306 | 2,859 | ||||
| 2,5 | 173,760 | 1,418 | |||
| 51,579 | 0,477 | ||||
| 3,2 | 38,215 | 0,241 | 118,4 | ||
| 3,5 | 10,124 | 0,036 | |||
| 4,9 | 7,942 | 1,462 | 225,4 | ||
| 219,579 | 1,714 | ||||
| 6,2 | 666,579 | 6,296 | 427,8 | ||
| 7,3 | 1355,579 | 13,026 | |||
| Итого: | 40,6 | 3475,636 | 37,309 | 2105,6 |
Тогда 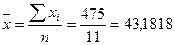 (млн. руб.);
(млн. руб.);
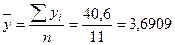 (млн. руб.);
(млн. руб.);
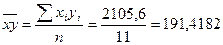 ;
;
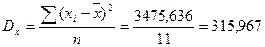 ;
; 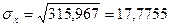 (млн. руб.);
(млн. руб.);
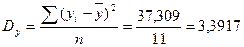 ;
; 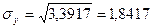 (млн. руб.);
(млн. руб.);
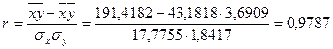 ;
;
Уравнение линейной регрессии имеет вид:
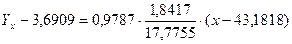 или
или 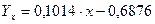 .
.
2а) Линейный коэффициент корреляции между переменными x и y равен 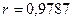 , что свидетельствует о прямой весьма высокой связи между этими признаками, т.е. между объемом реализованной продукции и балансовой прибылью предприятия.
, что свидетельствует о прямой весьма высокой связи между этими признаками, т.е. между объемом реализованной продукции и балансовой прибылью предприятия.
2б) Найдем коэффициент корреляции знаков Фехнера.
В таблице 8.3 запишем знаки отклонений индивидуальных величин от средней.
Таблица 8.3
| x | y | Знак 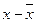
| Знак 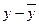
| «с» - совпадение знаков «н» - несовпадение знаков |
| 1,2 1,8 2,0 2,5 3,0 3,2 3,5 4,9 5,0 6,2 7,3 | ─ ─ ─ ─ ─ ─ ─ + + + + | ─ ─ ─ ─ ─ ─ ─ + + + + | с с с с с с с с с с с |
Итак, число совпадений знаков отклонений 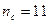 и число несовпадений знаков отклонений
и число несовпадений знаков отклонений 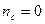 . Тогда
. Тогда 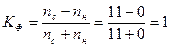 . Следовательно, между изучаемыми признаками существует прямая тесная корреляционная связь.
. Следовательно, между изучаемыми признаками существует прямая тесная корреляционная связь.
2в) Найдем коэффициент корреляции рангов Кендалла.
В таблице 8.4 запишем ранги переменных x и y.
Таблица 8.4
| x | y | Ранг x | Ранг y |
| 1,2 1,8 2,0 2,5 3,0 3,2 3,5 4,9 5,0 6,2 7,3 |
Упорядочим все единицы по признаку x (см. табл. 8.5)
Таблица 8.5
| x | y | Ранг x | Ранг y |
| 1,2 1,8 2,5 2,0 3,0 3,2 3,5 4,9 5,0 6,2 7,3 |
По признаку y подсчитаем суммы P и Q:
P= 10+9+7+7+6+5+4+3+2+1+0=54, Q= 0+0+1+0+0+0+0+0+0+0+0=1.
Тогда 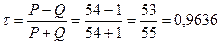 . Следовательно, между изучаемыми признаками существует прямая тесная корреляционная связь.
. Следовательно, между изучаемыми признаками существует прямая тесная корреляционная связь.
2г) Найдем коэффициент корреляции рангов Спирмена.
Рассчитаем в таблице квадраты разностей между рангами переменных x и y (см. табл. 8.6).
Таблица 8.6
| x | y | Ранг x | Ранг y | (Ранг x – Ранг y)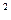
|
| 1,2 1,8 2,5 2,0 3,0 3,2 3,5 4,9 5,0 6,2 7,3 | ||||
| Итого: |
Тогда 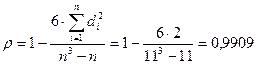 . Следовательно, между изучаемыми признаками существует прямая тесная корреляционная связь.
. Следовательно, между изучаемыми признаками существует прямая тесная корреляционная связь.
3) Коэффициент детерминации найдем по формуле:
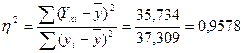 ,
,
необходимые суммы рассчитаны в таблицах 8.7 и 8.2.
Таблица 8.7
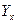
| 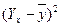
| 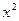
| 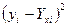
| |
| 1,340 | 5,525 | 0,020 | ||
| 1,847 | 3,399 | 0,002 | ||
| 2,354 | 1,786 | 0,021 | ||
| 2,760 | 0,867 | 0,577 | ||
| 2,963 | 0,530 | 0,001 | ||
| 3,064 | 0,393 | 0,018 | ||
| 3,368 | 0,104 | 0,017 | ||
| 3,977 | 0,082 | 0,853 | ||
| 5,193 | 2,258 | 0,037 | ||
| 6,309 | 6,853 | 0,012 | ||
| 7,424 | 13,937 | 0,015 | ||
| Итого: | 40,6 | 35,734 | 1,575 |
следовательно, модель объясняет зависимость между переменными на 95,78 %.
4а) При уровне значимости 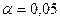 проверим гипотезу о значимости линейного коэффициента корреляции.
проверим гипотезу о значимости линейного коэффициента корреляции.
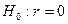 ,
,
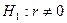 .
.
1. Наблюдаемое значение критерия
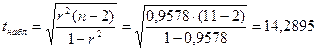 .
.
2. Критическая точка 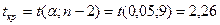 .
.
3. Т.к. 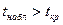 (14,2895>2,26), то отклоняем нулевую гипотезу об отсутствии связи между показателями x и y. Т.е. полученное значение r считается значимым, и принимаем гипотезу о наличии статистической связи между показателями.
(14,2895>2,26), то отклоняем нулевую гипотезу об отсутствии связи между показателями x и y. Т.е. полученное значение r считается значимым, и принимаем гипотезу о наличии статистической связи между показателями.
4б) При уровне значимости 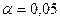 проверим гипотезу о значимости простой линейной регрессии.
проверим гипотезу о значимости простой линейной регрессии.
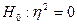 ,
,
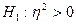 .
.
1. Наблюдаемое значение критерия
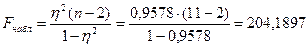 .
.
2. Критическая точка 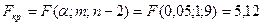 .
.
3. Т.к. 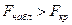 (204,1897>5,12), то отклоняем нулевую гипотезу о равенстве нулю коэффициента детерминации. Т.е. принимаем конкурирующую гипотезу о значимости линейной регрессии между показателями x и y.
(204,1897>5,12), то отклоняем нулевую гипотезу о равенстве нулю коэффициента детерминации. Т.е. принимаем конкурирующую гипотезу о значимости линейной регрессии между показателями x и y.
4в) При уровне значимости 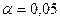 проверим гипотезы о значимости параметров регрессии.
проверим гипотезы о значимости параметров регрессии.
Для коэффициента регрессии b:
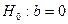 ,
,
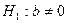 .
.
1. Наблюдаемое значение критерия
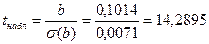 ,
,
где 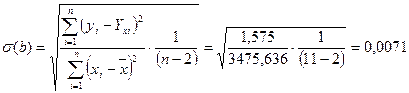 (необходимые суммы найдены в таблицах 8.2 и 8.7);
(необходимые суммы найдены в таблицах 8.2 и 8.7);
2. Критическая точка 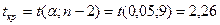 .
.
3. Т.к. 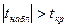 (14,2895>2,26), то отклоняем нулевую гипотезу о незначимости коэффициента регрессии, т.е. коэффициент регрессии не равен нулю.
(14,2895>2,26), то отклоняем нулевую гипотезу о незначимости коэффициента регрессии, т.е. коэффициент регрессии не равен нулю.
Для параметра a:
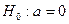 ,
,
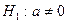 .
.
1. Наблюдаемое значение критерия
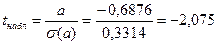 ,
,
где 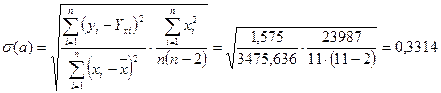 (необходимые суммы найдены в таблицах 8.2 и 8.7);
(необходимые суммы найдены в таблицах 8.2 и 8.7);
2. Критическая точка 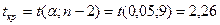 .
.
3. Т.к. 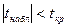 (|-2,075|<2,26), то принимаем нулевую гипотезу о незначимости параметра a, т.е. параметра a почти не отличается от нуля или равен нулю, и он может не использоваться в модели. Однако наличие свободного члена в линейном уравнении может лишь уточнить вид зависимости. Поэтому, если нет серьезных причин для удаления свободного члена из уравнения регрессии, то лучше его использовать в модели.
(|-2,075|<2,26), то принимаем нулевую гипотезу о незначимости параметра a, т.е. параметра a почти не отличается от нуля или равен нулю, и он может не использоваться в модели. Однако наличие свободного члена в линейном уравнении может лишь уточнить вид зависимости. Поэтому, если нет серьезных причин для удаления свободного члена из уравнения регрессии, то лучше его использовать в модели.
5) Точечный прогноз балансовой прибыли при объеме реализации, равном 75 млн. руб. найдем по построенной модели:
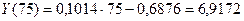 (млн. руб.)
(млн. руб.)
Доверительный интервалдля прогнозного значения 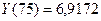 млн. руб. будет иметь вид:
млн. руб. будет иметь вид:
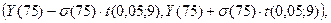
где
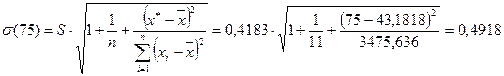 ,
,
стандартная ошибка регрессии 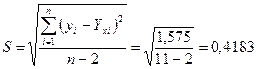 .
.
Т.к. 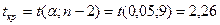 , то доверительный интервал будет иметь вид:
, то доверительный интервал будет иметь вид:
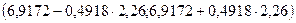 или
или 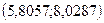 .
.
Таким образом, при уровне значимости 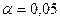 при объеме реализации, равном 75 млн. руб. балансовая прибыль предприятия ожидается в пределах от 5,8057 млн. руб. до 8,0287 млн. руб.
при объеме реализации, равном 75 млн. руб. балансовая прибыль предприятия ожидается в пределах от 5,8057 млн. руб. до 8,0287 млн. руб.
Если связь между признаками выражается какой-либо кривой линией, то нужно применить соответствующую формулу для расчета уравнения регрессии. Так, например, при связи, выраженной в форме гиперболы, уравнение регрессии имеет вид:
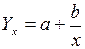 ,
,
Параметры уравнения 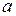 и
и 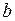 находятся из решения системы уравнений:
находятся из решения системы уравнений: 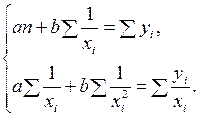
Если уравнение регрессии имеет форму параболы второго порядка, то его уравнение будет: 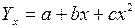 .
.
Параметры уравнения 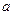 ,
, 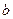 и
и 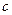 находятся из решения системы уравнений:
находятся из решения системы уравнений: 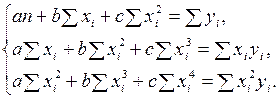
Показателем тесноты криволинейной корреляции является корреляционное отношение, которое вычисляется по выше приведенной формуле.
 2014-02-10
2014-02-10 529
529








