2014-02-12
348
В случае, если число испытаний п велико, а вероятность появления события А постоянна и отлична от нуля, то вероятность того, что событие А в серии из n испытаний произойдет ровно m раз приближенна равна значению функции
= 
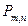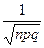f(х), где f(х) =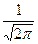 
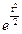, t =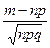 
,
где функция f(х)- табулированная функция., четная.Эта формула дает результат достаточной точности, если выполнено условие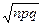 
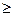15.
Формула Пуассона (формула малых вероятностей)
=
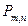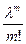e
, 
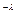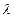= np.
Вероятностный смысл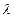- это среднее число появления события А в испытаниях.
Значения функции Пуассона для различных 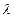и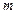 
приведены в таблицах. Формула обеспечивает достаточно высокую точность при выполнении условий n
,
.
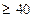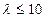Если вероятность наступления события А в п независимых испытаниях постоянна и равна р и отлична от 0 и 1, то вероятность того, что событие А появится в п испытаниях не менее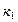 
раз, но не более 
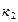раз приближенно вычисляется по интегральной теореме Лапласа:
Р (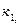
,) = 
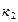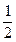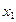(Ф(
)-Ф(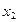
)), Ф(х)=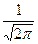 
,
=
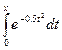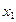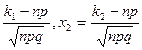
Значения функции Ф(х) табулированы для различных х. При пользовании таблицей следует учитывать, что эта функция нечетная. Достаточная точность формулы обеспечивается при условии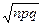 
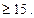
Пример. Найти вероятность того, что соб
ытие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события к в каждом испытании равна 0,2.
Решение. По условию п=400, к=80,р=0,2.
Воспользуемся асимптотической формулой Лапласа:
=
= 
.
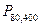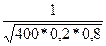
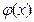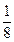
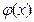Вычислим определяемое данными значение х: х=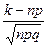
=
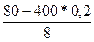=0
По таблице находим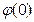 
=0,3989. Искомая вероятность 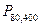= 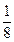*0,3989= 0,04986.
Пример. Вероятность поломки одной дорожной балки 0,1. Найти вероятность того,что из 100 балок сломаются не более 15.
Решение. P=0,1, q=0,9, =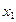
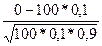=-3,3333
=
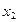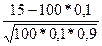=1,667,Ф(3,3333)=-Ф(3,3333)= -0,4995, Ф(1,667)= 0,4526
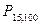=0,4526+ 0,4995= 0,9521.
Пример. Вероятность того,что на базу прибудет неисправный товар 0,003. Найти вероятность того, что на базу придет 4 неисправных товара из 100.
Решение. P=0,003,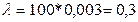 
. 
=
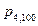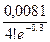=0,00002.
