Формула полной вероятности. Повторные независимые испытаний

План лекции.

Повторные независимые испытаний

Лекция 2.

1.Формула полной вероятности.

2.Формула Бейеса.

3.Повторение испытаний.

4. Формула Бернулли. Наивероятнейшее число появлений событий.

5.Локальная и интегральная формулы Лапласа.

6.Вероятность отклонения относительной частоты от постоянной вероятности.

7. Теорема Пуассона.

Литература: [1], [2], [3], [4].

Пусть событие А может наступить при условии появления одного из несовместных событий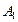,,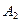…,,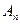 которые образуют полную группу событий. Пусть известны вероятности этих событий и условные вероятности события А.

Теорема. Вероятность появления события А, которое может наступить лишь при появлении одного из несовместных событий 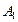,,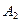…,,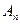 образующих полную группу событий, равна сумме произведений вероятностей каждого из этих событий на соответсвующую вероятность события А:

Р(А) = Р (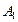)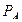(А) + Р (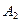) 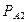(А) + Р (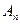) 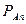(А).

Полученная формула называется формулой полной вероятности.