Формулы Бейеса

Пусть событие А может наступить при условии появления одного из несовместных событий 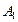,,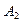…, , 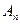образующих полную группу событий. Посколько заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности.

Допустим далее, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились вероятности гипотез. Другими словами будем искать условные вероятности (), (.),…,().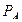

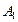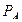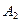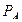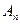Найдем сначала условную вероятность 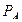(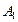). По теореме умножения имеем:

Р (А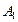) = Р (А) 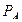(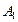) = Р (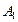)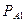(А).

Отсюда

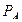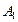()= Р(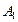)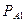(А)/ Р(А).- формулы Бейеса.

Аналогично выводятся формулы для определения условных верояостей других гипотез.

Формулы гипотез позволяют переоценить вероятности гипотез после того как становится известным результат испытания, в итоге которого появилось событие А.