2014-02-12
617
Теорема 1. Пусть(1)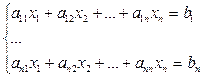 
- система n линейныхуравнений с n неизвестными над полем P, А=
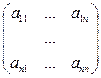- основнаяматрица системы(1), 
=
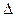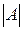. Если 
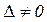,то система(1) имеетединственное решение: 
, 
, …, 
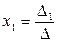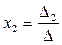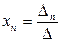,где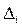 
- определитель,полученный из 
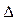заменой i- гостолбца на столбец свободных членов, i=
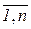,т.е.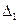 
=
, …, 
=
.
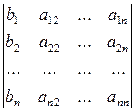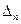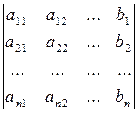Доказательство. Пусть Х =
, В =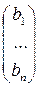
. Тогда система (1) равносильна матричному уравнению АХ=В (2).
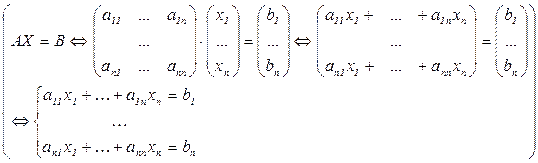
Следовательно, чтобы решить систему (1), достаточно решить уравнение (2). Так как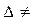 
0, то существует А-1 и уравнение (2) имеет единственное решение X=A-1B =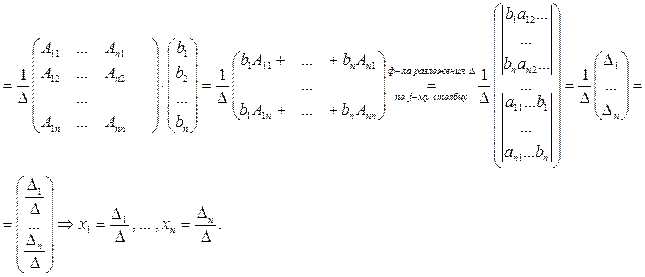 
Теорема доказана.
Замечание. Если 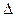= 0, то возможны 2 случая:
1. Если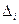 
= 0, i =
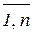, то система (1) имеет бесконечное число решений
2. Если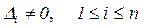 
, то система (1) не имеет решений.
