Простейшие свойства векторного пространства

Пусть V — векторное пространство над полем Р. Тогда справедливы следующие свойства.

Свойство 1. Для любого из V 0×= , где 0 — ноль поля Р, — нулевой элемент аддитивной группы V, т. е. ноль-вектор.

Доказательство. 0×= (0 + 0) = А₄ = 0×+ 0×, т.е. 0×= 0×+ 0×(1)

С другой стороны 0×= 0×+ (2)

Из (1) и (2) 0×+ = 0×+ 0×. В илу закона сокращения в аддитивной группе V, получим 0×= . Свойство доказано.

Свойство 2. Для любого a из Р a×=.

Доказательство. a×=a×(+ )= А₃ = a×+ a×(3)

a×= a×+ (4)

Из (3) и (4) a×+ = a×+ a×. Проводя левостороннее сокращение, из последнего равенства получим a×= . Свойство доказано.

Свойство 3. Если a= (5), то либо a=0 либо = .

Доказательство. Если a = 0, то требуемое равенство верно. Если a ¹ 0, то существует a^-1 Î Р. Умножим обе части равенства (5) слева на a^-1. Получим a^-1(a) = a^-1, откуда, по А₂ и свойству 2,

(a^-1a) = Û 1×= Û (по А₅) = . Свойство доказано.

Свойство 4. Для любого из V выполняется -1×= -.

Доказательство. = (свойство 1)= 0×= (1+(-1)) = А₄ = 1×+ (-1)× = А₅ = + (-1)× . Прибавим к обеим частям последнего равенства слева -. Получим (-1)×= -. Свойство доказано.

Следствие 1. Для любого a из Р, для любого из V выполняется (-a)= -a .

Следствие 2. Для любых a и b из Р, для любого из V выполняется (a - b)= a - b .

Свойство 5. Для любого a из Р, для любых 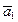, , 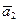…, 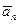из V выполняется

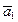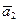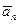a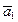(+ + … + ) = a+ a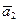+ … + a.

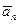Свойство 6. Для любых a₁, a₂, …, a_n из Р, для любого из V выполняется

(a₁ + a₂ + … + a_n) = a₁+ a₂+ … + a_n.