Формула для вычисления обратной матрицы

Теорема 1. Пусть A=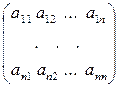- матрица n- го порядка над полем P.

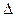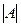
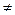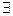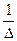
Если определитель =0, то А^-1, причем А^-1=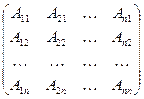, где А_ij - алгебраическое дополнение к элементу а_ij в матрице А, i=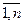, j=.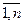

Доказательство. Так как 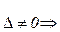А – невырожденная матрица. Тогда, по теореме 3, А – обратимая матрица. Значит, А^-1 существует. Пусть B =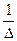 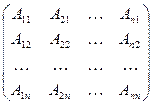. Покажем, что В=А^-1, т.е. покажем, что АВ=ВА=Е_n. Действительно,

АВ ==

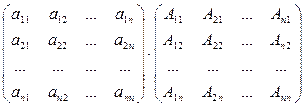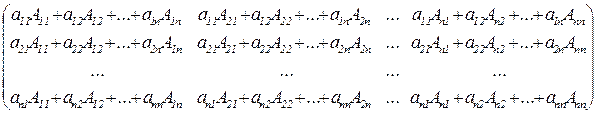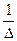
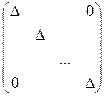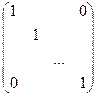== = = E_n, т.е. АВ=Е_n (1). Аналогично доказывается, что ВА=Е_n (2). Из (1) и (2) следует, что В=А^-1. Теорема доказана.