1)  +
+  =
=  +
+  - коммутативность.
- коммутативность.
2)  + (
+ ( +
+ 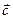 ) = (
) = ( +
+  )+
)+ 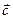
3)  +
+ 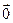 =
= 
4)  +(-1)
+(-1) =
= 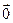
5) (a×b) = a(b
= a(b ) – ассоциативность
) – ассоциативность
6) (a+b) = a
= a + b
+ b - дистрибутивность
- дистрибутивность
7) a( +
+  ) = a
) = a + a
+ a
8) 1× =
= 
Определение.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
3) Базисом на прямой называется любой ненулевой вектор.
Определение. Если 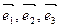 - базис в пространстве и
- базис в пространстве и 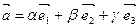 , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора  в этом базисе.
в этом базисе.
В связи с этим можно записать следующие свойства:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
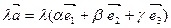 =
= 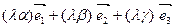 .
.
- при сложении векторов складываются их соответствующие компоненты.
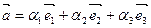 ;
; 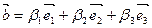 ;
;
 +
+  =
= 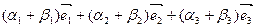 .
.
 2014-02-12
2014-02-12 413
413








