Векторное произведение векторов. Определение. Векторным произведениемвекторов и называется вектор , удовлетворяющий следующим условиям

Определение. Векторным произведением векторов и называется вектор 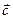, удовлетворяющий следующим условиям:

1) 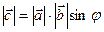, где j - угол между векторами и ,

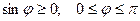
2) вектор 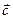ортогонален векторам и

3) , и 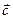образуют правую тройку векторов.

Обозначается: 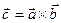или.

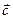
j

Свойства векторного произведения векторов:

1) ;

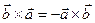2) 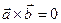, если ïïили = 0 или = 0;

3) (m)´= ´(m) = m(´);

4) ´(+ ) = ´+ ´ ;

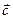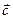5) Если заданы векторы (x_a, y_a, z_a) и (x_b, y_b, z_b) в декартовой прямоугольной системе координат с единичными векторами 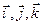, то

´=

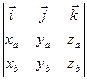
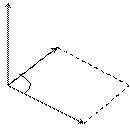
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .

Пример. Найти векторное произведение векторов и

.

= (2, 5, 1); = (1, 2, -3)

.

Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),С(0, 1, 0).

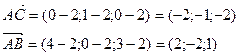
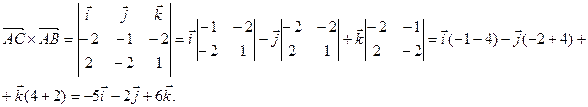
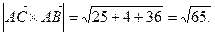
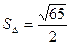(ед²).

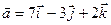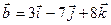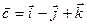Пример. Доказать, что векторы , и компланарны.

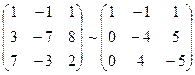, т.к. векторы линейно зависимы, то они компланарны.

Пример. Найти площадь параллелограмма, построенного на векторах 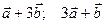, если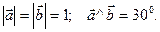

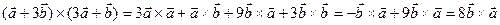
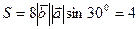(ед²).