Деревья решений

Приведенная выше табл. 2.1 может быть представлена в виде дерева решений (рис. 2.3). На этом дереве квадратик озна­ чает место, где решение принимает человек, а светлый кру­ жок - место, где все решает случай. На ветвях дерева написа­ ны уже знакомые нам значения вероятностей, а справа у конеч­ ных ветвей - значения исходов (результаты).

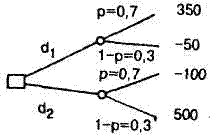
Рис. 2.3. Дерево решений

Для чего нужно дерево решений? Мы можем использовать его для представления своих возможных действий и для нахо­ ждения последовательности правильных решений, ведущих к максимальной ожидаемой полезности. Чтобы показать это, ус­ ложним задачу. Пусть в вазе 1-го типа содержится 6 красных и 4 черных шара. В вазе второго типа содержится 3 красных и 7 черных шаров. Предоставим человеку, выбирающему между действиями d 1 и d 2, дополнительные возможности. Пусть он может до своего ответа вытащить за определенную плату один шар из вазы, причем после вытаскивания шар кладется обрат­но в вазу. Плата за вытаскивание одного шара равна 60 д. е.

Дерево решений с двумя его основными ветвями представ­ лено на рис. 2.4. Вот теперь вопрос о том, какое решение сле­ дует принимать, стал сложнее: необходимо решить, стоит ли вынимать шар и какой ответ дать после вытаскивания красно­ го или черного шара. При принятии этих решений нам окажет существенную помощь известный в теории вероятностей [4] (и в теории статистических решений) способ подсчета изменения вероятностей событий после получения дополнительной ин­ формации.

Вернемся к описанию задачи. Вероятность вытащить крас­ ный шар из вазы 1-го типа p K (B 1)=0,6, а из вазы 2-го типа p к (В 2)=0,3. Зная все условные вероятности (зависящие от усло­ вия), а также вероятности p 1 и p 2 выбора ваз 1-го и 2-го типа (см. табл. 2.1), мы можем поставить следующие вопросы.

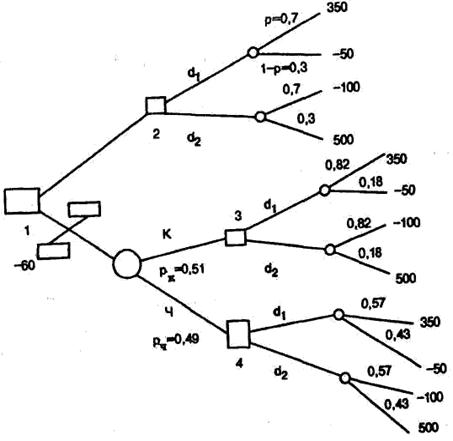
Рис. 2.4. Дерево решений

Первый вопрос: каковы вероятности вытащить красный и черный шары? Для ответа на этот вопрос произведем простые вычисления. Вероятность вытащить красный шар: p K (B 1)=0,7 A 0,6=0,42, если ваза окажется 1-го типа, p к (В 2)=0,3 A 0,3=0,09, если ваза окажется 2-го типа. Следовательно, вероятность вы тащить красный шар в общем случае р к =0,51. Аналогичным образом можно посчитать, что вероятность вытащить черный шар Рч=0,49.

Второй вопрос более сложный. Пусть вытащенный шар оказался красным (черным). Какое действие следует выбрать: d 1 или d 2? Для ответа на этот вопрос нужно знать вероятности принадлежности ваз к 1-му и 2-му типам после получения до­ полнительной информации. Эти вероятности позволяет опреде лить знаменитая формула Байеса [4].

Например, мы вытащили красный шар. Какова после этого вероятность того, что перед нами стоит ваза 1-го типа?

Приведем все обозначения вероятностей:

• p k (B 1) - вероятность вытащить красный шар из вазы 1-го типа;
• p ч (B 1) — вероятность вытащить черный шар из вазы 1-го типа;
• p к(В 2) ~ вероятность вытащить красный шар из вазы 2-го типа;
• p ч (В 2) — вероятность вытащить черный шар из вазы 2-го типа;
• p (B 1) - вероятность того, что ваза окажется 1-го типа;
• р(В 2) - вероятность того, что ваза окажется 2-го типа;
• p (B 1/ K) - вероятность того, что ваза окажется 1-го типа по­ сле вытаскивания красного шара;
• p (B 1/ч) - вероятность того, что ваза окажется 1-го типа по­сле вытаскивания черного шара;
• р(В 2/к) - вероятность того, что ваза окажется 2-го типа по­ сле вытаскивания красного шара;
• p (В 2/ч) - вероятность того, что ваза окажется 2-го типа по­ сле вытаскивания черного шара.

Формула Байеса позволяет оценить p (B i / K) и p (B i /ч), где i =1, 2, используя все прочие вероятности. Например:

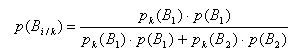
Для нашей задачи: p (B 1/ K)=0,82; p (B 1/ч)=0,57; p (B 2/ K)=0,18; р(В 2/ч)=0,43.

Теперь мы имеем всю информацию, необходимую для при нятия решений.

На рис. 2.4 показаны две основные ветви дерева решений, причем верхняя просто повторяет дерево решений на рис. 2.3. Квадратик 1 слева соответствует первому решению - вытаски вать шар или нет. Случаю отказа от вытаскивания шара соот­ ветствует верхняя основная ветвь. Решению вытаскивать шар соответствует нижняя ветвь, начинающаяся со случайного со бытия (кружок). В квадратиках 2, 3, 4 принимаются решения о выборе одной из двух стратегий: d 1 или d 2. Далее все решает случай (кружки).

Есть три простых правила выбора оптимальной (по крите-, рию максимума ожидаемой полезности) последовательности ре-шений на основе дерева решений:

• идти от конечных ветвей дерева к его корню;

• там, где есть случайность (кружок), находится среднее значение;

• там, где есть этап принятия решений (квадратик), выбирается ветвь с наибольшей ожидаемой полезностью, а другая отсекается двумя черточками.

Применим эти правила к дереву решений, представленному на рис. 2.4. В результате получим дерево решений, показанное на рис. 2.5.

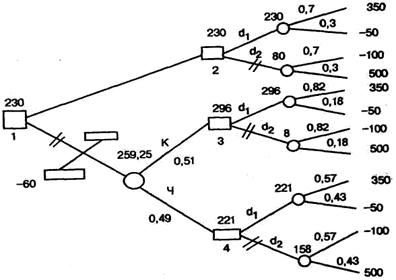
Рис. 2.5. «Сворачивание» дерева решений

На этом рисунке над кружками указаны средние значения полезности, двумя черточками отсечены ветви с меньшим значением ожидаемой полезности. Наилучший вариант действий: шар не вытаскивать и выбирать действие d 1. Этот вариант соот­ ветствует самому верхнему пути дерева решений на рис. 2.5. Такая процедура нахождения оптимального пути на деревьях решений получила название «сворачивание» дерева решений.

Деревья решений при заданных числовых значениях веро­ ятностей и исходов позволяют осуществить выбор той страте­ гии (последовательности действий), при которой достигается наибольший выигрыш, т.е. достигается максимум функции по лезности ЛПР.