Построение перпендикуляров к плоскости, перпендикулярных прямых и перпендикулярных плоскостей является основными графическими операциями при решении метрических задач.
Прямой угол между перпендикулярными прямыми общего положения на плоскости проекций проецируется с искажениями, поэтому задачу о построении перпендикуляра к прямой общего положения решают с помощью условия перпендикулярности прямой и плоскости.
Рассмотрим случай построения перпендикуляра из точки А к прямой общего положения m.
Эта задача решается следующей последовательностью графических операций:
- Через точку А проводится плоскость Q, перпендикулярная прямой m.
- Определяется точка встречи прямой m с плоскостью Q. K=m
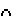 Q.
Q.
Для этого проводят вспомогательную плоскость S. m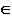 S; l=S
S; l=S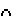 Q.
Q. - Соединяют точку А с точкой К. АК
 m, так как он лежит в плоскости, перпендикулярной прямой m.
m, так как он лежит в плоскости, перпендикулярной прямой m.
Таким образом, две прямые перпендикулярны, если одна из них лежит в плоскости, перпендикулярной другой прямой.
Чтобы посмотреть, как эти построения выполнить на эпюре, рассмотрим пример:
Даны прямая общего положения m и точка А. Требуется опустить перпендикуляр из точки А на прямую m.
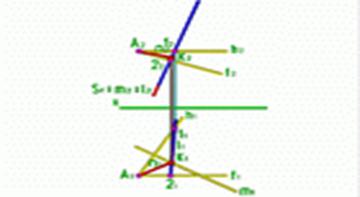 Рис.5
Рис.5
| Q(h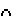 f) A f) A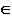 Q; f2 Q; f2 m2 h1 m2 h1 m1 Q m1 Q m; m m; m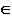 S; l=S S; l=S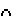 Q K=m Q K=m l AK l AK m. m.
|
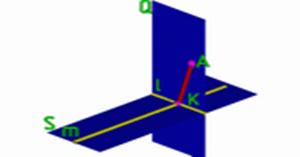 Рис.6
Рис.6
|
 2014-02-12
2014-02-12 665
665








