Две плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости.
Поэтому построение плоскости Р, перпендикулярной к плоскости Q, можно осуществить двумя путями:
- Проводим прямую m, перпендикулярную к плоскости Q, затем прямую m заключаем в плоскость Р.
(m Q)
Q)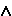 (m
(m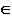 P)
P)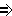 P
P Q
Q - Проводим прямую n, перпендикулярную или параллельную плоскости Q, затем строим плоскость Р, перпендикулярную к прямой n.
(n Q)
Q)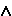 (n
(n P)
P)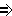 P
P Q
Q
Так как через прямую m можно провести множество плоскостей (первый путь решения) и в плоскости или параллельно её можно провести множество прямых n (второй путь решения), то задача имеет множество решений.
Поэтому для получения единственного решения нужно наложить дополнительные условия, например, потребовать, чтобы плоскость Р проходила через точку А, принадлежащую другой плоскости (Q).
Пример: Даны плоскость Р (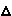 ABC) и точка D. Нужно через точку D провести плоскость Q
ABC) и точка D. Нужно через точку D провести плоскость Q Р.
Р.
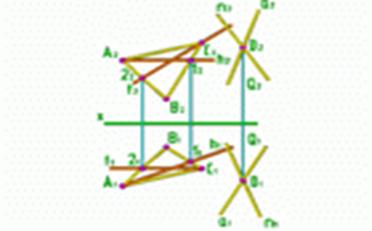 Рис.7
Рис.7
| a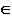 Q, D Q, D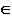 a. Плоскость P удобно задать: [C1] a. Плоскость P удобно задать: [C1]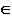 h [A2] h [A2]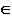 f n2 f n2 f2 n1 f2 n1 h1 (D h1 (D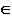 n) Q(n n) Q(n a) a)
|
Рассмотрим случай когда горизонтально проецирующая плоскость S перпендикулярна к плоскости общего положения P.
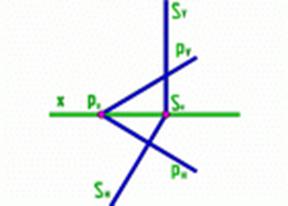 Рис.8
Рис.8
| Если (S H) H) (S (S P), то S P), то S PH, как к линии пересечения плоскостей P и H. PH=P PH, как к линии пересечения плоскостей P и H. PH=P H. Отсюда PH H. Отсюда PH S и, следовательно PH S и, следовательно PH SH, как к одной из прямых в плоскости S. SH, как к одной из прямых в плоскости S.
|
Однако, если одноимённые следы двух плоскостей общего положения взаимно перпендикулярны, то сами плоскости не перпендикулярны между собой, так как при этом не соблюдается условие перпендикулярности плоскостей.
| IV МЕТОДЫ ПРЕОБРАЗОВАНИЯ ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ 1. Метод замены плоскостей проекций: 1.1 Замена фронтальной плоскости проекций. 1.2 Замена горизонтальной плоскости проекций. 1.3 Основные задачи замены плоскостей проекций. | Лекции: 1 2 3 4 5 6 7 8 9 10 11 12 13 |
 2014-02-12
2014-02-12 585
585








