При пересечении поверхности вращения плоскостью могут получиться следующие кривые:
а). Цилиндр вращения:
- эллипс - когда секущая плоскость
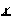 и
и 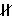 оси вращения.
оси вращения. - окружность - когда секущая плоскость
 оси вращения.
оси вращения. - две
 прямые - когда секущая плоскость
прямые - когда секущая плоскость  оси вращения.
оси вращения. - прямая линия - когда секущая плоскость касательна к поверхности цилиндра.
б). Конус вращения:
Поверхность прямого кругового конуса является носителем кривых 2-го порядка: окружности, эллипса, параболы, гиперболы, которые поэтому также называются коническими сечениями.
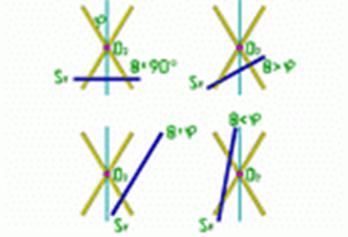 Рис.1 Рис.1 |
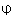 - угол наклона образующей конуса к его оси.
- угол наклона образующей конуса к его оси.
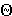 - угол наклона между секущей плоскостью и той же осью.
- угол наклона между секущей плоскостью и той же осью.
- эллипс - когда секущая плоскость пересекает все образующие конуса (т.е.
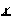 и
и 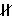 ).
). 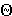 >
>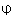
- окружность - когда секущая плоскость
 оси вращения.
оси вращения. 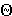 >
>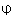 I,
I, 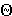 =90
=90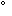
- парабола - когда секущая плоскость
 одной образующей конуса.
одной образующей конуса. 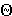 =
=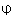
- гипербола - когда секущая плоскость
 оси вращения конуса или каким-либо двум образующим конуса.
оси вращения конуса или каким-либо двум образующим конуса. 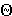 <
<
- две пересекающиеся прямые, прямая или точка, когда секущая плоскость проходит через вершину конуса.
Чтобы построить линию пересечения поверхности вращения плоскостью, необходимо:
- Ввести ряд вспомогательных плоскостей.
- Построить линии пересечения вспомогательной плоскости с заданными плоскостью и поверхностью.
- Определить точки взаимного пересечения построенных линий, которые принадлежат искомой линии пересечения.
Выбор вспомогательных плоскостей производится из следующих соображений:
- Вспомогательные плоскости при пересечении с заданной поверхностью должны давать линии пересечения простого вида (прямая, окружность).
- В результате применения вспомогательных плоскостей должны получаться точки, принадлежащие кривой сечения, наиболее характерные для этой кривой.
К характерным точкам кривой сечения относятся:
- высшая и низшая точки сечения;
- точки, разделяющие видимую и невидимую части сечения;
- точки, являющиеся концами большой и малой осей эллипса (в некоторых случаях эти точки могут совпадать).
4. Развёртка поверхностей вращения.
Дано: Прямой круговой конус, стоящий на плоскости проекций H, рассечён плоскостью общего положения P.
Нужно:
- Построить линию сечения конуса плоскостью.
- Определить видимость сечения и конуса на H и V.
- Построить истинную величину сечения.
- Построить развёртку нижней отсечённой части конуса.
Задача пересечения конуса плоскостью решается следующим образом:
- Для удобства делим горизонтальную проекцию основания (окружность) на 8 частей.
- Большая ось эллипса находится на прямой проходящей через вершину конуса и перпендикулярной горизонтальному следу секущей плоскости Р.
- Разделив большую ось пополам можно найти центр эллипса сечения - O.
- Если через точку O провести горизонтальную плоскость, то она пересекает заданный конус по окружности, а заданную плоскость P по горизонтали. В результате этого можно получить точки ограничивающие малую ось эллипса сечения.
- Проводим фронтальную плоскость T через вершину конуса. Вспомогательная плоскость T пересекает конус по очерковым образующим S1 и S5, а заданную секущую плоскость по фронтали. В результате этого получаем точки a и d, принадлежащие кривой сечения и определяющие границу видимости этой кривой на фронтальной плоскости проекций.
- Для построения промежуточных точек b, c, e, f находим точки пересечения соответсвующих образующих с секущей плоскостью.
Натуральную величину сечения определяем методом совмещения плоскости P с плоскостью H, для чего плоскость P вращаем вокруг её горизонтального следа.
Для построения развёртки:
- Поверхность конуса мысленно режем по образующей S1.
- Определяем угол кругового сектора
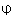
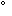 =180*D/L
=180*D/L - Зная угол кругового сектора, выполняем полную развёртку кругового сектора.
- Длину окружности основания конуса делим на равные части (чем больше, тем лучше).
- Дугу кругового сектора делим на такое же количество частей. На развёртке проводим образующие.
- На развёртке наносим точки сечения, которые находятся на образующих S1 - S8.
- Полученные точки на развёртке соединяем плавной кривой линией.
- К развёртке боковой поверхности конуса пристраиваем натуральные величины основания и сечения.
 Рис.2 Рис.2 |
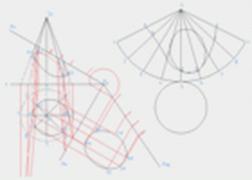 Рис.3 Рис.3 | ||
| 5. Взаимное пересечение поверхностей вращения. | Лекции: 1 2 3 4 5 6 7 8 9 10 11 12 13 | |
 2014-02-12
2014-02-12 851
851








