2014-02-12
617
Прямоугольные аксонометрические проекции - изометрия и диметрия. Коэффициент искажения (вывод) и углы между осями.
Отношение единичных отрезков на аксонометрических осях к единичным отрезкам на координатных осях называется коэффициентом искажения по аксонометрическим осям.
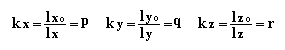
Очевидно, принимая различное взаимное расположение декартовой системы координат и картинной плоскости и задавая разные направления проецирования, можно получить множество аксонометрических проекций, отличающихся друг от друга как направлением аксонометрических осей, так и величиной коэффициента искажения вдоль этих осей.
Справедливость этого утверждения была доказана немецким геометром Карлом Польке. Теорема Польке утверждает:
"Три отрезка произвольной длины, лежащие в одной плоскости и выходящие из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трёх равных отрезков, отложенных на прямоугольных осях координат от начала."
На основании этой теоремы аксонометрические оси и коэффициенты искажения по ним могут выбираться произвольно. Если коэффициенты искажения приняты различными по всем трём осям, т.е. p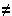
q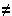r, то эта аксонометрическая проекция называется триметрической. Если коэффициенты искажения одинаковы по двум осям, т.е. p=r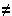q, - диметрической. Если коэффициенты искажения равны между собой, т.е. p=q=r, - изометрической.
В машиностроении наибольшее распространение получили (см. ГОСТ 2317-69):
- Прямоугольная изометрия: p=r=q,
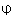=90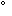
. - Прямоугольная диметрия: p=r, q=0.5p, 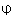=90.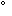
- Косоугольная фронтальная диметрия: p=r, q=0.5p, <90.
