2014-02-12
756
Обратное преобразование
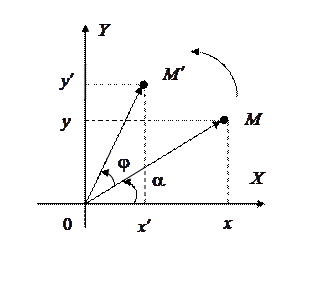
Обратное преобразование соответствует повороту системы координат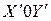 
на угол 
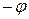. Соответствующие выражения для преобразования координат могут быть получены из (8.19) – (8.23) путем замены в них 
→ 
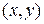и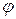 
→ 
.
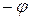Матрица преобразования будет иметь вид
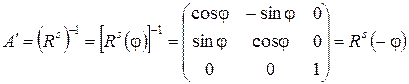(8.24)
Под преобразованием объектов будем понимать изменение координат точек, принадлежащих этому объекту при изменении его положения в некоторой системе координат.
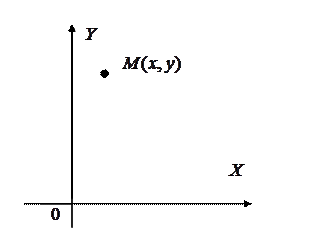
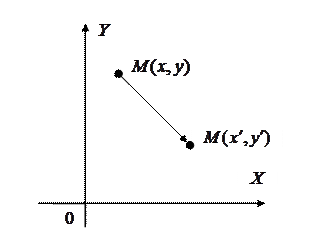
Пусть в системе координат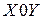 
некоторая точка 
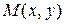перемещается из положения 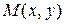в положение 
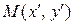(рис. 4а, 4б) или обратно из положения 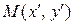в положение .
| 
|
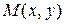| Рис. 8.5а | Рис. 8.5б |
Тогда старые координаты точки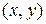
и новые 
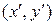связаны соотношениями (8.1) – (8.8). Подчекнем лишь, что в данном случае выражения (8.1) – (8.8) описывают взаимосвязь между старыми и новыми координатами точки 
при изменении ее положения в одной и той же системе координат.
Рассмотрим частные случаи аффинных преобразований объектов.
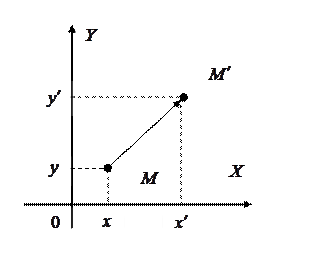
Сдвиг объекта (рис. 8.6)
| 
|
| Рис. 8.6 | Рис. 8.7 |
Из рис. 8. 6 получаем
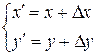, (8.25)
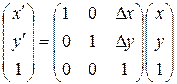(8.26)
или
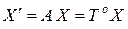, (8.27)
где
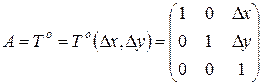(8.28)
Здесь и далее индекс «
» означает, преобразованию подвергаются координаты объекта.
