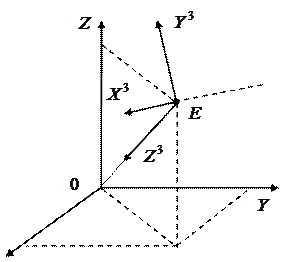
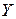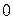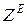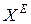Для изображения объекта на экране его мировые координаты необходимо преобразовать (пересчитать) в другую систему координат, которая связана с точкой наблюдения. Эта система координат называется видовой системой координат и является левосторонней.
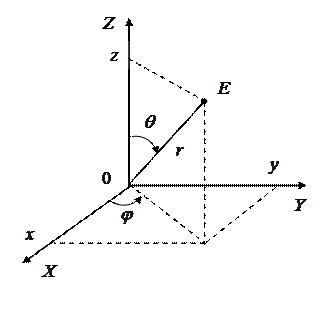 | 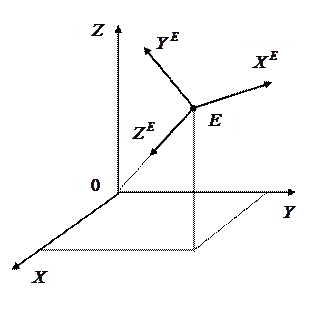 |
| Рис. 10.2 | Рис. 10.3 |
Рассмотрим правую систему мировых координат 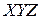 (рис. 2) и зададим в ней точку наблюдения
(рис. 2) и зададим в ней точку наблюдения 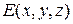 , где
, где
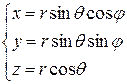 (10.1)
(10.1)
Система видовых координат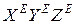 показана на рис. 10.3.
показана на рис. 10.3.
Преобразование мировых координат в видовые можно представить в виде
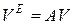 , (10.2)
, (10.2)
где 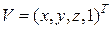 – координаты некоторой точки в мировой системе координат,
– координаты некоторой точки в мировой системе координат, 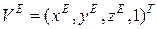 – координаты этой же точки в видовой системе координат,
– координаты этой же точки в видовой системе координат, 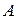 – матрица преобразования.
– матрица преобразования.
Получим выражение для матрицы 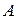 , выполняя переход от мировой системы координат к видовой путем последовательности элементарных преобразований.
, выполняя переход от мировой системы координат к видовой путем последовательности элементарных преобразований.
Сместим начало системы координат 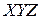 (рис. 10.2) в точку
(рис. 10.2) в точку 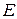 (рис. 10.4), переход
(рис. 10.4), переход 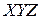 →
→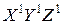 .
.
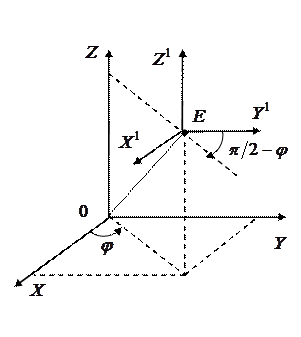 | 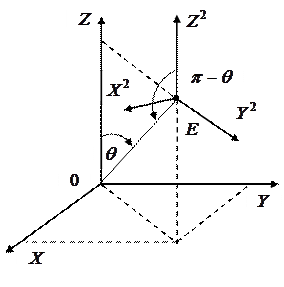 |
| Рис. 10.4 | Рис. 10.5 |
Преобразование координат имеет вид
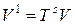 , (10.3)
, (10.3)
где
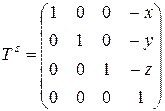 , (10.4)
, (10.4)
где 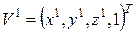 .
.
Повернем систему координат 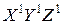 (рис. 10.4) вокруг оси
(рис. 10.4) вокруг оси 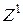 на угол
на угол 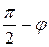 , переход
, переход 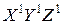 →
→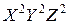 (рис. 10.5).
(рис. 10.5).
Преобразование координат имеет вид
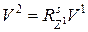 , (10.5)
, (10.5)
где 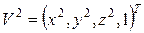 .
.
Поскольку поворот выполняется по часовой стрелке (в отрицательном направлении), то в матрице преобразования 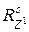 (9.33) следует использовать аргумент
(9.33) следует использовать аргумент 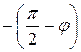 . В результате матрица преобразования примет вид
. В результате матрица преобразования примет вид
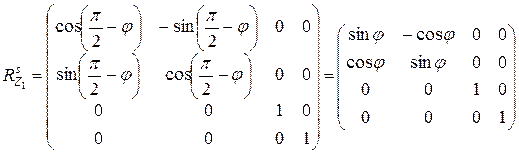 (10.6)
(10.6)
Повернем систему координат 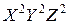 (рис. 10.5) вокруг координатной оси
(рис. 10.5) вокруг координатной оси 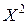 на угол
на угол 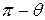 , переход
, переход 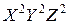 →
→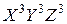 (рис. 10.6)
(рис. 10.6)
|   


| |||||||||||||||||||||||||||||
| Рис. 10.6 | Рис. 10.7 |
Преобразование координат имеет вид
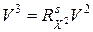 , (10.7)
, (10.7)
где 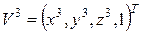 .
.
В результате матрица преобразования примет вид
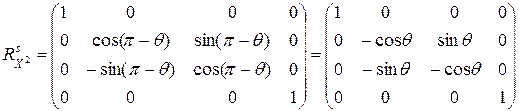 . (10.8)
. (10.8)
Изменим направление оси 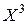 (рис. 10.6) на противоположное
(рис. 10.6) на противоположное 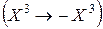 , переход
, переход 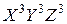 →
→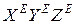 (рис. 10.7).
(рис. 10.7).
Преобразование координат имеет вид
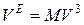 , (10.9)
, (10.9)
где
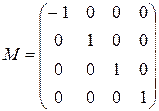 (10.10)
(10.10)
– матица преобразования для перехода 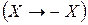
Выражение (10.9) с учетом (10.3), (10.5), (10.7) и (10.10) можно представить в виде
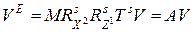 , (10.11)
, (10.11)
где
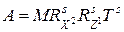 (10.12)
(10.12)
Подставляя в (10.12) выражения для матриц (10.4), (10.6), (10.8) и (10.10), получим
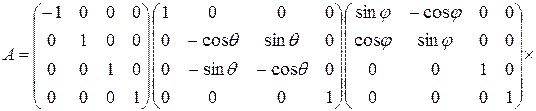
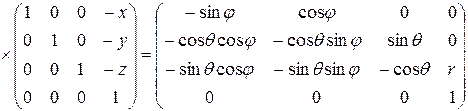 (10.13)
(10.13)
При получении (10.13) учтено, что элементы матрицы 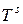
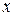 ,
, 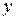 и
и 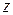 определяются выражениями (10.1).
определяются выражениями (10.1).
Таким образом, преобразование (10.2), связывающее координаты мировой и видовой систем координат можно представить в виде
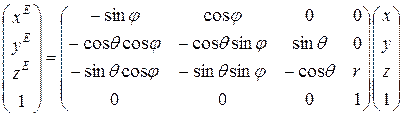 (10.14)
(10.14)
или
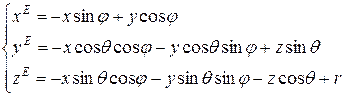 (10.15)
(10.15)
 2014-02-12
2014-02-12 6601
6601