2014-02-12
1572
Рассмотрим, как вычисляются координаты объекта в картинной плоскости, когда лучи проецирования исходят из одной точки, расположенной на конечном расстоянии от объекта (и плоскости проецирования), рис. 10.8.
Пусть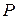 
– картинная плоскость в видовой системе координат 
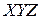(плоскость проецирования – 
), 
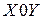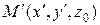– координаты некоторой точки, полученные пересчетом ее мировых координат в видовую систему координат 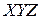без учета перспективы (аксонометрическая проекция) в соответствии с выражениями (15). Далее, пусть 
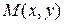– проекция точки 
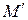на картинную плоскость 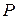, полученная с учетом перспективы, 
– 
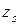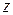- координата точки схода лучей. Необходимо вычислить координаты точки 
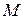, полагая, что координаты точки 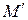являются известными.
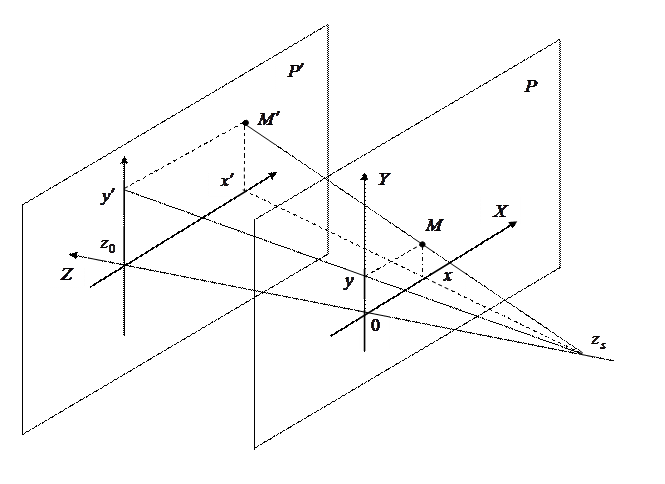
Рис. 10.8
Из подобия треугольников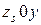 
и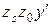 
получаем пропорцию
(10.16)
Откуда находим
(10.17)
Аналогично из подобия треугольников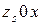 
и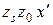 
получим
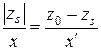(10.18)
и
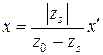(10.19)
Вводя обозначения
, (10.20)
можно записать
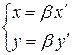(10.21)
Последние выражения можно записать в матричном виде
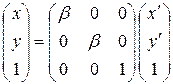(10.22)
или
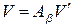, (10.23)
где
, 
,
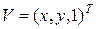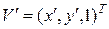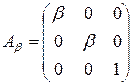(10.24)
Таким образом, этапы преобразования координат, при переходе от мировых координат к экранным, можно отобразить в виде блок-схемы, которая показана на рис. 10.9.
Сначала мировые координаты преобразуются в видовые с началом в точке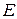 
(рис. 10.3). Затем при необходимости выполняется перспективное преобразование, добавляющее эффект перспективы. При построении аксонометрической проекции перспективное преобразование не выполняется и видовые координаты 
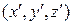(рис. 10.9) сразу используются для получения соответствующих оконных координат.
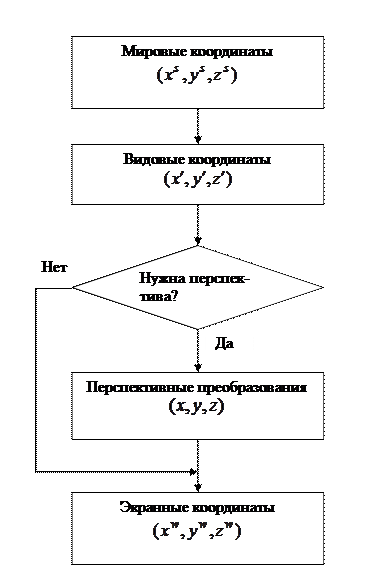
Рис. 10.9
