Применения
Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.
Пусть для функции f(x) известны значения yj = f(xj) в некоторых точках. Тогда мы можем интерполировать эту функцию как
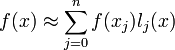
В частности,
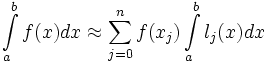
Значения интегралов от lj не зависят от f(x), и их можно вычислить заранее, зная последовательность xi.
В случае равномерного распределения узлов интерполяции xi выражаются через расстояние между узлами интерполяции h и начальную точку x0:
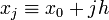 ,
,
и, следовательно,
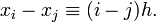
Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим
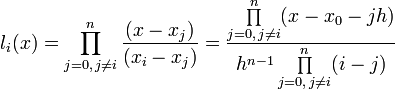
Теперь можно ввести замену переменной
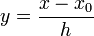
и получить полином от y, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования алгоритмов с многобайтным представлением чисел.
Тема 5.2. Блок-схема алгоритма и программа интерполяции методом Лагранжа
Постановка задачи
Предположим, что задано 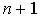 различных точек плоскости:
различных точек плоскости:
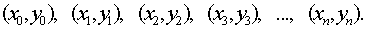 (1)
(1)
Требуется найти функцию 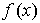 , значения которой при данных значениях абсциссы
, значения которой при данных значениях абсциссы 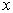
в точности равны соответствующим ординатам заданных точек:
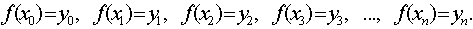
Т.е. нужно найти линию, описываемую уравнением 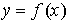
, проходящую через 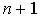 данную точку (рис.1).
данную точку (рис.1).
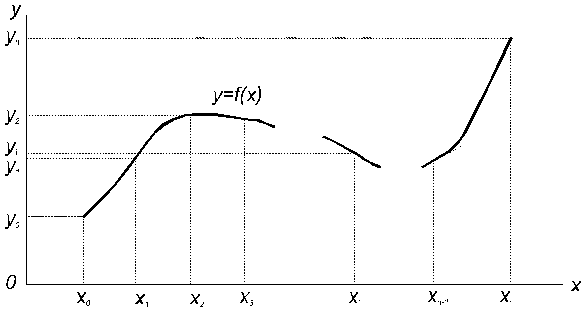
Рис.1
Заметим, что здесь приходится различать два случая:
1) интерполяцию (от лат. interpolar — подновлять) —восстановление промежуточных значений функции внутри интервала 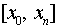 по ряду известных ее значений;
по ряду известных ее значений;
2) экстраполяцию (лат. приставка extra означает «вне») — когда не вошедшее в исследование значение 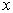 лежит вне интервала
лежит вне интервала 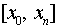 .
.
Очевидно, интерполяция более надежна, чем экстраполяция.
Вообще говоря, существует бесконечное число линий, проходящих через 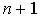 заданную точку. Потребуем, чтобы искомая линия была простейшей, т.е. значения функции, задающие эту линию, должны находиться при помощи простейших операций (сложения, умножения). Этому требованию отвечают многочлены (полиномы), т.е. выражения вида:
заданную точку. Потребуем, чтобы искомая линия была простейшей, т.е. значения функции, задающие эту линию, должны находиться при помощи простейших операций (сложения, умножения). Этому требованию отвечают многочлены (полиномы), т.е. выражения вида:
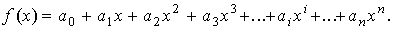 (2)
(2)
Зная численные значения коэффициентов 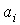 многочлена, мы можем найти его ординату при любом значении переменной
многочлена, мы можем найти его ординату при любом значении переменной 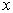 . Наконец, из двух многочленов условимся считать простейшим тот, степень которого ниже.
. Наконец, из двух многочленов условимся считать простейшим тот, степень которого ниже.
Итак, приходим к задаче о полиномиальной интерполяции: пусть даны 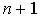
различных чисел 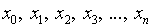 и
и 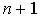 соответствующих им чисел
соответствующих им чисел 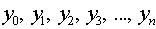 , требуется найти многочлен
, требуется найти многочлен 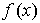 наименьшей возможной степени, удовлетворяющий
наименьшей возможной степени, удовлетворяющий 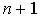 условиям:
условиям:
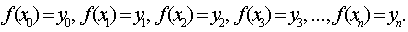
 2014-02-12
2014-02-12 1562
1562
