Тема 6.1. Метод Эйлера

Раздел 6. Формирования математических моделей с помощью дифференциальных уравнений

Способы интерполяции

1.Интерполяция многочленами

На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций.

2. Обратное интерполирование (вычисление x при заданном y)

3. Интерполяция функции нескольких переменных

4. Другие способы интерполяции

См. https://ru.wikipedia.org/wiki

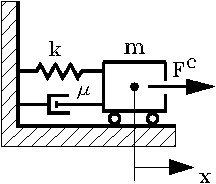Вернемся к рассмотрению системы на рис.1.1.

Рис. 1.1

Перепишем еще раз уравнение равновесия:

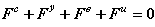(2.1)

Поскольку при численном интегрировании мы получаем решение в отдельных точках временной оси, то для каждого i-го момента времени уравнение (2.1) может быть записано в виде:

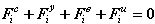, (2.2)

где

,

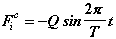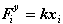, (2.3)

,

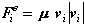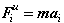
Считаем также, что для i-го момента времени значения xi, vi, ai связаны уравнениями (1.7), которые ввиду их использования в наших дальнейших выкладках воспроизведем еще раз:

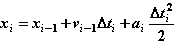(2.4)

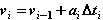
Обратите внимание, что уравнения (2.3) отличаются от аналогичных выражений (1.3) знаком. Это связано с тем, что в PRADIS при рассмотрении условий равновесия суммируются усилия, действующие со стороны системы на элементы, а не усилия со стороны элементов, как это было принято нами при выборе положительного направления для сил в соответствии с рис. 1.3.

Подстановкой (2.3) в (2.2) можно было бы получить уравнение вида (1.8), но мы этого делать не будем, поскольку нам нужно формировать и анализировать математическую модель по универсальному алгоритму. Итак, имеем достаточно универсальное уравнение равновесия вида (2.2), справедливое для каждого i-го момента времени. Заметим, что переход от записи уравнения равновесия в форме (2.1) к записи в форме (2.2) ознаменовал собой качественное изменение типа уравнения. Если соотношение (2.1) представляет собой дифференциальное уравнение (поскольку входящие в него зависимости для сил используют производные перемещения по времени), то соотношение (2.2) есть уже просто алгебраическое нелинейное уравнение (поскольку связь между xi, vi, ai определяется алгебраическими уравнениями (2.4)). А с нелинейным уравнением в форме (2.2) можно поступать также, как мы поступаем с уравнением (1.12), а именно: решать его методом Ньютона.

Имеем

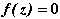, (2.5)

где

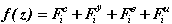
Переменной z мы можем обозначить любую из компонент xi, vi или ai, поскольку они взаимосвязаны соотношениями (2.4). Примем, как и раньше, z=vi.

На каждой итерации, в соответствии с формулами (1.14), нам необходимо вычислить значение f(z) и ее производной df(z)/dz.

Вычисление f(z) сводится к суммированию текущих значений сил при текущих значениях xi, vi, ai (i - номер шага по времени, j - номер итерации по Ньютону). Фактически, вычисляемое значение f(z) представляет собой погрешность выполнения условия равновесия, которую ньютоновскими итерациями необходимо "загнать" в допустимые пределы.

Теперь распишем производную df(z)/dz.

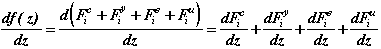(2.6)

Действуя строго по науке, каждую из производных в выражении (2.6) мы должны представить как производную сложной функции.

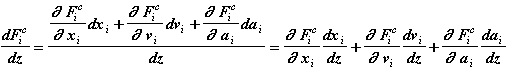
Так как z=vi, то

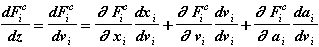(2.7)

Аналогично:

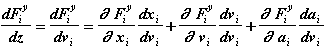
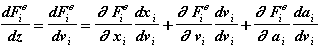(2.7a)

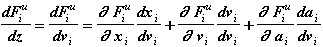
Используем уравнения связи (2.4) для получения зависимостей ai и xi от vi:

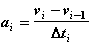, (2.8)

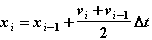
Продифференцируем выражения (2.8) по vi

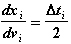
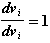
(2.9)

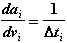
Теперь вычислим частные производные в выражениях (2.7), (2.7а), пользуясь зависимостями (2.3):

Для силы Fiс:

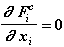(Fiс не зависит от перемещения тела)

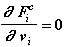(Fiс не зависит от скорости тела) (2.10)

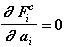(Fiс не зависит от ускорения тела)

Для силы Fiу:

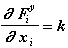
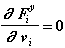(Fiу не зависит от скорости тела) (2.11)

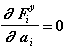(Fiу не зависит от ускорения тела)

Для силы Fiв:

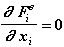(Fiв не зависит от перемещения тела)

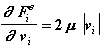(2.12)

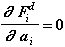(Fiв не зависит от ускорения тела)

Для силы Fiи:

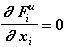(Fiи не зависит от перемещения тела)

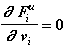(Fiи не зависит от скорости тела) (2.13)

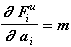
Подставляем полученные значения частных производных от усилий и значения коэффициентов (2.9) в формулы (2.7), (2.7а):

,

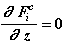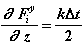, (2.14)

,

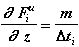
Суммируем слагаемые формулы (2.6):

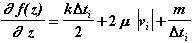(2.15)

Сравнивая результат с ранее полученной формулой (1.19), для которой коэффициенты берутся из соотношений (1.12), можно констатировать, что они похожи.

Теперь, имея возможность вычислять f(z) и df(z)/dz, продолжить расчет по описанному ранее алгоритму не представляет труда. Однако, как говорил один их героев Толкиена, "ситуация в настоящий момент может представляться требующей некоторых разъяснений ". Продравшись через частокол полных и частных производных, мы получили тот же результат, что и ранее, но терпения у читателя эти выкладки наверняка изрядно поубавили. Какими же приобретениями окупаются эти трудозатраты?

1. Дифференциальное уравнение движения выписывать вообще не пришлось.

2. Развернутая форма нелинейного уравнения вида (1.12), к решению которого сводится расчет на каждом шаге по времени, тоже оказалась невостребованной.

3. Функциональная зависимость для производной df(z)/dz не понадобилась.

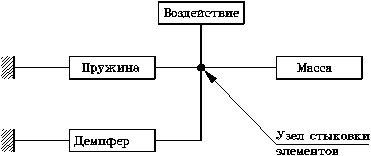
Рис. 2.1

Если внимательно просмотреть наши рассуждения, то мы использовали следующую информацию (приводимый ниже список необходимой для формирования математической модели информации будем далее называть "перечнем"):

1. Сведения о стыковке элементов схемы (рис. 2.1).

2. Условие равновесия сил, записанное для i-го момента времени, и представляющее собой нелинейное алгебраическое уравнение относительно xi, vi, ai вида:

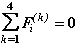, (2.16)

где 4 - количество сил, сходящихся в узле стыковки (количество стыкующихся ветвей элементов).

Уравнение (2.16) еще называют топологическим, поскольку оно определяется топологией, т.е., структурой связей в схеме.

3. Выражения, позволяющие определить усилия в каждом элементе как функцию перемещения, скорости, ускорения и времени - (2.3). Это так называемые компонентные уравнения, описывающие поведение отдельной компоненты (элемента) схемы.

4. Выражения для частных производных от усилий, действующих в элементе, по перемещению, скорости, ускорению - см. зависимости (2.10)-(2.14).

5. Алгебраические уравнения связи x, v, a для текущего момента времени - формулы метода интегрирования (2.4).

6. Указание, относительно какой из переменных - x, v или a - вести решение нелинейного уравнения, т.е., что выбирается в качестве переменной z функции f(z) в формуле (2.5).

Перечисленной информации достаточно для реализации машинных алгоритмов формирования математической модели объекта.

Чтобы у читателя не осталось темных мест и белых пятен, мы еще раз более детально пройдемся по уже неоднократно разобранному в этом документе примеру.

Итак, пусть имеется техническая система, процессы в которой требуют анализа. Расчетная схема соответствует рис.1.1.

Систему необходимо представить в виде совокупности элементов,стыкующихся по общим степеням свободы (узлам). Количество степеней свободы (узлов) у каждого элемента определяется разновидностью элемента (рис. 2.2).

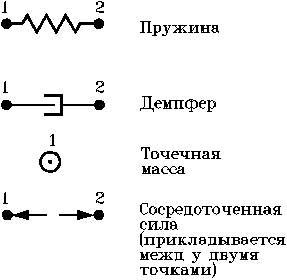
Рис. 2.2

Существует понятие модели элемента. Пользователь собирает модель системы из моделей отдельных элементов, как игрушку в детском конструкторе. Его (пользователя) должна заботить только правильность сборки, остальные вопросы формирования математической модели - головная боль разработчиков программного обеспечения. Имея перед собой расчетную схему (рис. 1.1) и вычленив из нее элементы (рис. 2.2), пользователь находит модели соответствующих элементов в библиотеке моделей элементов программного комплекса и описывает структуру исследуемой схемы.

Описание структуры заключается в соединении элементов по общим степеням свободы и указании закрепленных узлов. Для полноты картины приведем кусок текста описания структуры на входном языке PRADIS:

$ FRAGMENT: Пример

# BASE: 1

# STRUCTURE:

Пружина' K (1 2; Коэффициент жесткости)

Нелинейный демпфер ' MUNL (1 2; Коэффициент вязкости)

Масса ' M (2; Масса тела)

Воздействие ' FSIN (2 1; Q, T, начальная фаза)

Подготовкой приведенного описания пользователь сообщил программному комплексу PRADIS всю необходимую информацию по стыковке элементов схемы (см. пункт 1 перечня необходимой информации для формирования математической модели объекта). Пользователь, во-первых, подобрал модели элементов из библиотеки моделей - это модели K, MUNL, M, FSIN. Во-вторых, соединил их надлежащим образом, приложив воздействие к массе в узле 2, к которому также присоединил концы пружины и демпфера. Наконец, описал узел 1 как неподвижный, закрепив тем самым свободные концы пружины и демпфера.

Рассмотрим теперь те действия программы, которые позволяют в целом представить механизм работы вычислительного алгоритма.

В процессе обработки описания структуры модели определяется размерность системы уравнений, т.е., количество узлов, в которых должны выполняться условия равновесия. В рассматриваемом примере два узла, один из которых закреплен. На стадии формирования математической модели структура данных будет готовиться по обоим узлам, однако на этапе расчета уравнение, соответствующее закрепленному узлу, исключается из рассмотрения, и все кинематические характеристики закрепленного узла (перемещение, скорость, ускорение) устанавливается в ноль.

Этап численного интегрирования представляет собой последовательность шагов по времени, каждый из которых сводится к решению нелинейного уравнения равновесия вида (2.16). Для решения этого уравнения необходима информация, приведенная выше в пунктах 3-6 перечня.

Сейчас самое время обратить внимание на модели элементов и выяснить, какова их роль в вычислительном алгоритме. Входными данными для любой модели элемента являются:

- неизменный список параметров модели элемента;

- текущие значения перемещений, скоростей и ускорений тех узлов, с которыми этот элемент соединен.

По этим данным модель элемента обязана для текущего момента времени вычислить:

1) усилия, которые действуют со стороны системы на элементы, т.е., вектор усилий элемента (см. пункт 3 перечня);

2) частные производные вычисляемых усилий по перемещениям, скоростям и ускорениям узлов элемента, т.е., так называемую матрицу Якоби (якобиан) элемента (см. пункт 4 перечня).

Если элемент имеет N степеней свободы, то длина вектора усилий элемента также N, а якобиан элемента имеет длину N*N*3.

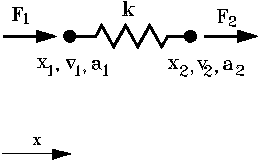
Рис. 2.3

Как это выглядит? Например, разработчик двухузловой модели одномерной безразмерной безинерционной идеально упругой пружины, которую мы используем в своем примере,

реализовал следующие зависимости для усилий и якобиана элемента (рис. 2.3):

,

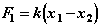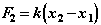(2.17)

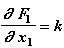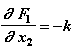, (2.18)

,

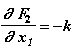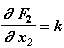
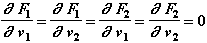(2.19)

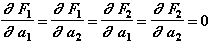(2.20)

В соответствии с приведенными зависимостями, для любого момента времени модель элемента по переданным в нее текущим значениям перемещений, скоростей и ускорений (хотя для рассматриваемого элемента важны только перемещения) вычисляет значения усилий, действующих на концы пружины, и значения частных производных от усилий по перемещениям, скоростям и ускорениям обоих узлов. Вектор усилий состоит их 2 элементов, якобиан - из 12.

Поскольку в рассматриваемой расчетной схеме объекта узел 1 пружины закреплен, то в данном конкретном случае из всей информации, вычисляемой моделью и передаваемой "наверх", востребуется только та часть, которая связана с незакрепленным вторым узлом:

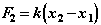(2.21)

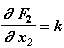(2.22)

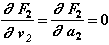
Эта информация позволяет учесть вклад пружины при решении нелинейного уравнения вида (2.5) по алгоритму, изложенному при выводе соотношений (2.6)-(2.15). Вклад остальных элементов (демпфер, масса, внешнее воздействие) учитывается аналогичным образом.

Чтобы конкретизировать сказанное, продолжим ранее начатое интегрирование примера, сделав очередной 3-й шаг по времени. При этом будем использовать формальный алгоритм, базирующийся на последовательности вычислений по формулам (2.5)-(2.15).

Напомним, что по результатам 2-го шага по времени (при t2=1.438e-3 с) мы получили следующие значения неизвестных:

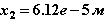
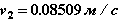
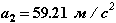
Величина шага равнялась ∆t2=0.438 e-3 с, полученное на шаге значение локальной погрешности составило lp2=0.000018.

Рекомендуемое значение ∆t3 для следующего шага определяем по формуле (1.30) с учетом c=0.8 и δl = 0.001:

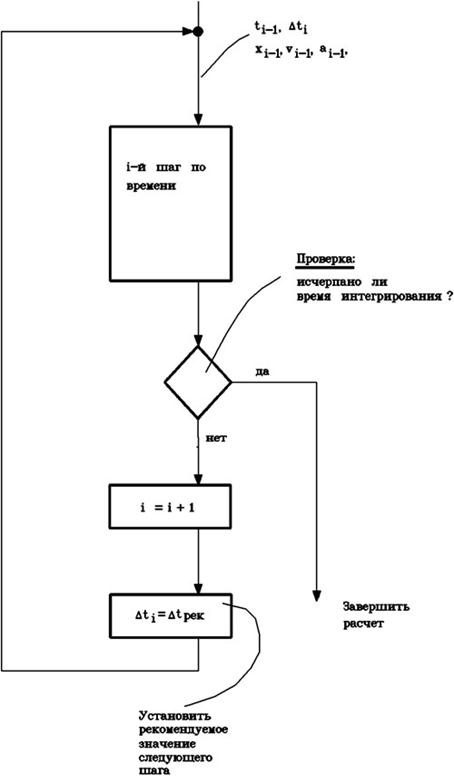
Дальше действуем по схеме, представленной на рисунках 2.4а-2.4в. Из рис. 2.4.а следует, что перед i-м шагом по времени должны быть известны значения ti-1, xi-1, vi-1, ai-1, ∆ti. Можно убедиться, что перед началом 3-го шага мы действительно располагаем информацией о значениях t2, x2, v2, a2, ∆t3.

Подробности алгоритма выполнения отдельного шага почерпнем из рис. 2.4.б.

1. Определяем значения коэффициентов приведения якобиана - 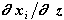, , 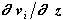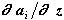(см. формулы (2.7), (2.7а)), зависящие от величины шага. Поскольку при расчетах на первых двух шагах за базисную переменную мы уже приняли скорость (т.е., z=vi), то суммирование якобиана проводится по формулам (2.7), (2.7а), для которых коэффициенты приведения вычисляются по зависимостям (2.9):

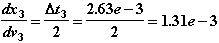
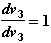
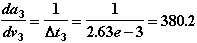
Напомним, что соотношения (2.9) определяются формулами метода интегрирования (2.4).

2.Вычисляем начальное приближение к решению по формуле явного прогноза (1.28):

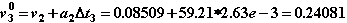
Обратите внимание, что в качестве начального приближения должно быть вычислено не только значение vi0, но и значения xi0, ai0, необходимые для расчета в моделях элементов.

Поэтому:

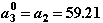
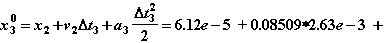
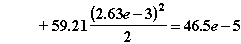
3. Установив счетчик итераций равным 1, реализуем последовательность действий на 1-й итерации Ньютона (см. рис. 2.4в).

4. Обращение к моделям элементов. Вычисление вектора сил и якобиана каждого элемента по текущим значениям x30, v30, a30.

В настоящий момент ограничимся анализом информации только по незакрепленному узлу:

Рис. 2.4а

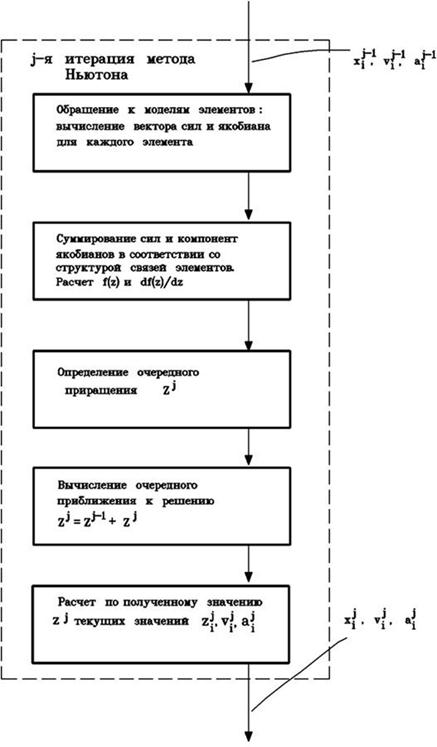
Рис. 2.4в

Пружина:

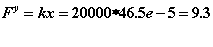
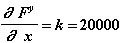
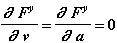
Демпфер:

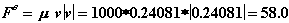
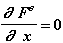
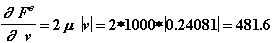
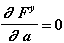
Точечная масса:

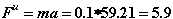
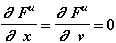
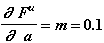
Прикладываемая сила:

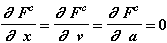
5. Суммируем силы, вычисленные в моделях элементов и сходящиеся в незакрепленном узле

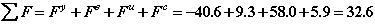
Полученная сумма является значением функции f(z) на текущей итерации (см. выражение (2.5)).

Вычислим теперь df(z)/dz, используя соотношения (2.6), (2.7), (2.7а):

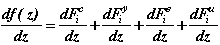
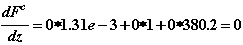
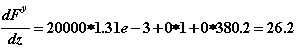
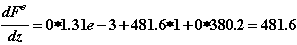
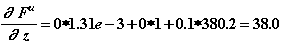
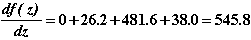
6.Определяем приращение :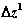

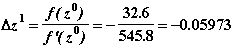
7. Вычисляем очередное приближение к решению

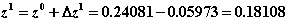
8. По полученному значению 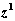уточняем текущие значения x31, v31, a31, используя формулы (2.81):

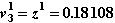
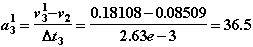
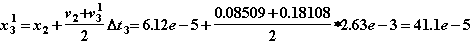
Вычисления на первой итерации Ньютона закончены.

9. Проверяем условия завершения ньютоновских итераций. Напомним, что ранее мы приняли следующие значения допустимых погрешностей для проверки условий (1.15):

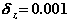
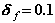
Исходя из этих значений, заключаем, что

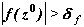
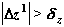
Таким образом, ньютоновские итерации на текущем шаге по времени необходимо продолжить.

10. Прежде, чем перейти на следующую итерацию, проверяем, не исчерпано ли предельное количество итераций:

j = 1 < jmax = 5

11. Увеличиваем счетчик номера итераций:

j = j + 1 = 1 + 1 = 2

12. Проверяем последовательность действий на рис. 2.4в для второй итерации метода Ньютона. Эти действия приведут нас к следующему решению:

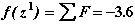
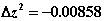
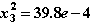
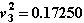
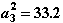
Проверка условий окончания итераций покажет, что итерации еще не закончены:

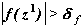
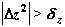
Проверка:

j = 2 < jmax = 5

устраняет последние преграды с пути выполнения очередной, третьей итерации.

13. Третья итерация окажется последней. Будет получен следующий результат:

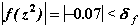
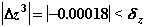
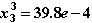
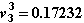
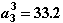
14. В соответствии со схемой 2.4б, после успешного завершения ньютоновских итераций необходимо оценить величину локальной погрешности на шаге интегрирования

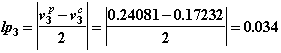
15. Вычисляем рекомендуемое по критерию локальной погрешности значение следующего шага.

Здесь следует вставить одну ремарку. Практика расчетов показала, что формула (1.30) приемлема только в определенном диапазоне соотношений δl / lpi, а именно - вблизи единицы. При значительных отличиях δl / lpi от единицы рекомендуемое формулой (1.30) значение шага, как правило, завышено и приводит к неоправданной потере шагов из-за неудовлетворения требованиям точности интегрирования. В этом мы убедимся уже сейчас, поскольку для выбора величины текущего шага использовали формулу (1.30) при соотношении δl / lpi = 0.001/0.000018 = 55.5. Как следствие этого, сделанный шаг с рекомендуемым формулой (1.30) значением шага ∆t3=2.63e-3 привел нас к результату, когда сравнение фактически полученной (lp3 = 0.034) и предельно допустимой (δl=0.001) локальных погрешностей определяет необходимость повторения расчетов на 3-м шаге с уменьшенным значением шага.

Скорректируем правило выбора шага по критерию локальной погрешности. Оно выглядит следующим образом:

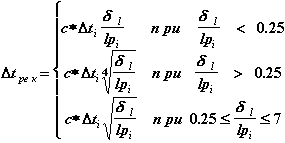(2.23)

Тогда, продолжая обсуждение алгоритма с прерванного места, рекомендуемое значение шага для повторного расчета на 3-м шаге определим с учетом (2.23):

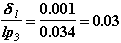
Поскольку δl / lp3 < 0.25, то

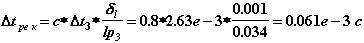
16. Устанавливаем ∆t3= 0.061*e-3 с и повторяем вычисления на 3-м шаге, начиная с пункта 1.

Повторный расчет с этим значением шага приводит к следующим результатам для момента времени t3=t2+ t3 = 1.499*e-3 с:

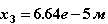
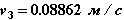
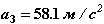
Локальная погрешность в пределах нормы. Рекомендуемое значение для следующего шага ∆tрек=0.264*e-3с.

Расчет на третьем шаге по времени закончен.

Основное, на что хотелось бы обратить внимание по завершении разбора примера, - это разделение функций между собственно программой интегрирования и программами реализации моделей элементов. Программе интегрирования, работающей по алгоритму рис. 2.4а-2.4в, вообще говоря, все равно, какие процессы интегрировать. Ее зависимость от моделей элементов сводится только к своевременному получению от них векторов сил и матриц якобианов. А какие свойства отдельных элементов эта информация отражает, программу интегрирования это касаться не должно. Модели элементов, в свою очередь, имеют свой уровень независимости информации при вполне очерченных обязанностях перед "верхами". То есть, физические свойства отдельного элемента объекта отражаются в компонентных уравнениях на уровне модели элемента, а программа интегрирования работает на уровне уравнений равновесия потоков, не касаясь, по каким соотношениям составляющие этих потоков вычисляются. Такое разграничение функций определяет универсальность вычислительного ядра PRADIS, т.е. принципиальную возможность расчета любых объектов, процессы в которых подчиняются законам равновесия потоковых переменных (равновесие сил, электрических и тепловых потоков, расходов жидкости и газа).

Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление», том 1, раздел 2, гл. 7. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно линейной функцией, т. н. ломаной Эйлера.