Прямые методы Рунге — Кутта

Классический метод Рунге — Кутта 4 порядка

Тема 6.3. Метод Рунге-Кутгы

Методы Рунге — Кутта — важное семейство численных алгоритмов решения (систем) обыкновенных дифференциальных уравнений. Данные итеративные методы явного и неявного приближенного вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методами Рунге — Кутта являются модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка (см. ниже). Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков.

Метод Рунге — Кутта 4 порядка столь широко распространен, что его часто называют просто метод Рунге — Кутта.

Рассмотрим задачу Коши 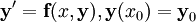. Тогда значение в следующей точке вычисляется по формуле:

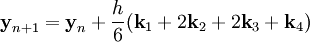
где

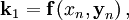
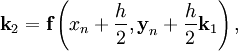
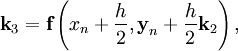
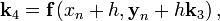
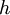— величина шага сетки по .

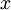Этот метод имеет 4 порядок, т.е. ошибка на каждом шаге составляет O(h5), а суммарная ошибка на конечном интервале интегрирования O(h4).

Семейство прямых методов Рунге — Кутта является обобщением метода Рунге — Кутта 4 порядка. Оно задается формулами

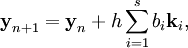
где

Конкретный метод определяется числом s и коэффициентами bi,aij и ci. Эти коэффициенты часто упорядочивают в таблицу

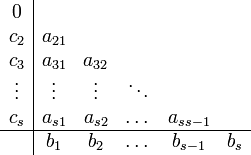
Для коэффициентов метода Рунге — Кутта должны быть выполнены услови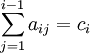я для 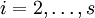. Если мы хотим, чтобы метод имел порядок 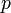, то следует так же обеспечить услови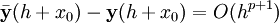е , где 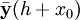— приближение полученное по методу Рунге — Кутта. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений на коэффициенты метода.