Процессы теплопереноса в недрах Земли

Как было отмечено ранее, теплообмен в горных породах осуществляется теплопроводностью, конвекцией и излучением. Применительно к задачам горного производства весьма важной является зада­ча регулирования теплового режима шахт и рудников при отработке глубоких горизонтов, а также при подземной разработке в условиях многолетнемерзлых пород.

Решение практических задач регулирования теплового режима шахт и рудников непосредственно связаны с процессами теплопере­носа в недрах Земли.

Процесс нестационарного теплопереносса теплопроводностью в земной коре за счет геотермического градиента описывается уравне­нием

.

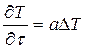При наличии внутриземных локальных источников теп­ла (например, в связи с окислительно-восстановительными реакци­ями) процесс теплопереноса описывается уравнением

.

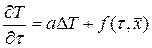В том случае, если к теплопереносу, обусловленному геотермическим гра­диентом, добавляется теплоперенос за счет конвекции (например, в связи с движением геотермальных вод), теплоперенос описывается уравнением

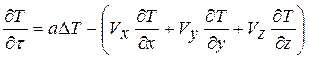
где - V_x, V_y, V_z компоненты скорости, с которой перемещается источник тепла.

И, наконец, теплоперенос за счет геотермическо­го градиента, конвекции, при наличии внутриземных локальных источников тепла и условии, что температуропроводность горных пород зависит от их температуры, описывается следующим уравне­нием:

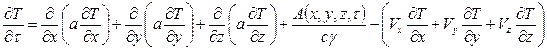(1.12)

Теплоперенос за счет решеточной составляющей теплопровод­ности и конвекции в основном формирует тепловой режим верхних слоев земной коры. На глубинах более 50 км в связи с высоким давлением и температурой теплоперенос осуществляется главным образом за счет электронной составляющей теплопроводности и теп­лообмена излучением.

С увеличением глубины и повышением температуры решеточ­ная составляющая теплопроводности уменьшается, а электронная увеличивается, поэтому на глубине около 100 км теплопроводность пород минимальна, что способствует дросселированию* оттока тепла из глубинных слоев Земли к ее поверхности.

Так как теплоемкость воды очень велика, то составляющая теплопереноса за счет конвекции при движении подземных вод оказы­вает существенное влияние в перераспределении тепловых потоков в верхних водонасыщенных слоях земной коры. Эта составляющая является определяющей в формировании непостоянного по глубине удельного теплового потока, который при наличии конвекции рас­считывается по формулам

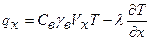; (1.13)

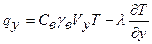; (1.14)

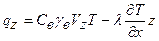, (1.15)

где С _в — удельная теплоемкость воды, Дж/ (кг·К); γ _в— плотность воды, кг/м³.

Для оценки температуры в земной коре при наличии водоносно­го горизонта рассмотрим следующую задачу: на некоторой глубине залегает водоносный горизонтальный пласт, скорость фильтрации воды в котором в вертикальном направлении равна V. Если за начало отсчета глубины принять поверхность Земли и ось Н направить вниз, то при отсутствии теплообмена в водоносном пласте в горизонталь­ной плоскости, что вполне допустимо, задачу теплопроводности мож­но считать одномерной относительно оси Н.

Обозначим координату кровли водоносного пласта через H₁, а почвы — через Н₂. При малой скорости фильтрации можно поло­жить, что температура жидкости равна температуре породы в каждой точке водоносного пласта. При данных условиях дифференциальное уравнение теплопроводности относительно оси Н с учетом конвекции для установившегося теплового режима в пласте имеет вид

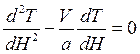
где а — температуропроводность водонасыщенных пород пласта, м²/с.

Зададим граничные условия задачи в виде

T=T₁ при Н=Н₁; (1.17)

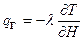, при Н=Н₂; (1.18)

где q_г— геотермический удельный тепловой поток, Вт/м²;

λ — теплопроводность водонасыщенных пород водоносного горизонта, Вт/(м·К).

Для нахождения решения уравнения (1.16) понизим его порядок, обозначив 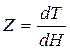, тогда уравнение (1.16) принимает вид линейного однородного уравнения первого порядка

,

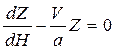разделяя в нем переменные

,

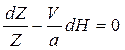и интегрируя, получим

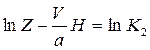или ,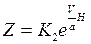

т.к. 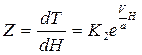, то разделяя переменные и, интегрируя его, получим общее решение уравнения (1.16) в виде

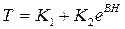(1.19)

где К₁ и К₂ — постоянные, определяемые из граничных условий, а В=V/ а.

При Н = Н₁ уравнение (1.19) примет вид

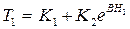(1.20)

Дифференцируя по Н общее решение (1.19), получим

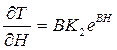(1.21)

Подставляя (1.21) в (1.18), получим при Н = Н₂

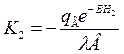(1.22)

Значение К₁ определим, подставив К₂ из (1.22) в (1.20), в ре­зультате получим

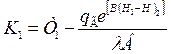(1.23)

Подставляя значение К₂ и К₁ из (1.22) и (1.23) в общее решение (1.19) в итоге получим уравнение для оценки распределения темпе­ратуры по толщине водоносного горизонта при граничных условиях (1.17) и (1.18)

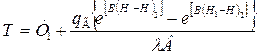(1.24)

Рассмотрим случай, когда на верхнем и нижнем уровнях водо­носного горизонта заданы граничные условия в виде

T=T₁ при Н=Н₁; (1.25)

Т = Т₂ при Н = Н₂; (1.26)

Решение дифференциального уравнения (1.16) - 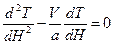как и в первом случае будем искать в виде (1.19) - .

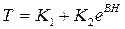Подставляя граничные условия (1.25) и (1.26) в общее решение (1.19), получим

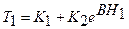(1.27)

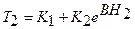(1.28)

Вычтя почленно из выражения (1.28) выражение (1.27), пол­учим

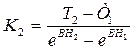(1.29)

Подставляя (1.29) в выражение (1.27), определим постоянную К₁

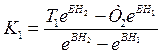(1.30)

Подставляя значения К₂ и К₁ из (1.29) и (1.30) в общее решение (1.19), получим

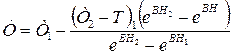(1.31)

Уравнение (1.31) позволяет определить распределение темпе­ратуры по толщине водоносного пласта при наличии фильтрации в нем и граничных условиях (1.25) - T=T₁ при Н=Н₁ и (1.26) - Т = Т₂ при Н = Н₂.

Продифференцировав уравнения (1.24)

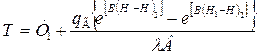
и (1.31) по Н, соответ­ственно получим

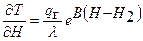(1.32)

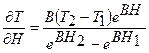(1.33)

Умножив левые и правые части уравнений (1.32) и (1.33) на λ, получим выражения для оценки удельных тепловых потоков по вы­соте водоносного горизонта при фильтрации в нем воды со скоростью V соответственно при граничных условиях (1.17)-(1.18) и (1.25)-(1.26).

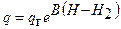(1.34)

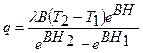(1.35)