Наиболее известным алгоритмом разложения матрицы на произведение ортогональной и треугольной матриц является алгоритм Грамма-Шмидта.
Вариант ортогонализации по столбцам. Суть алгоритма основана на утверждении, что всякую неособенную матрицу  можно представить в виде произведения матрицы
можно представить в виде произведения матрицы 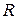 с ортогональными столбцами на верхнетреугольную матрицу
с ортогональными столбцами на верхнетреугольную матрицу 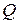 с единичной диагональю либо в виде произведения ортонормальной по столбцам матрицы
с единичной диагональю либо в виде произведения ортонормальной по столбцам матрицы 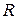 на обычную верхнетреугольную матрицу
на обычную верхнетреугольную матрицу 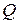 :
:
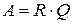 . (6.55)
. (6.55)
Представим исходную матрицу как совокупность векторов-столбцов
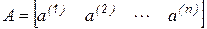 ,
,
где 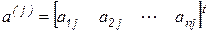 ;
; 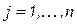 .
.
Т.к. матрица  неособенная, то векторы
неособенная, то векторы 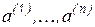 линейно независимы. Будем искать матрицу
линейно независимы. Будем искать матрицу 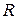 в виде
в виде
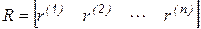 ,
,
где 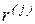 – искомые ортогональные столбцы.
– искомые ортогональные столбцы.
Вначале положим 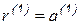 . Следующий вектор
. Следующий вектор 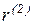 должен быть построен из
должен быть построен из 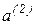 ортогонально
ортогонально 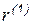 . Для этого вектор
. Для этого вектор 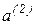 разложим на составляющие:
разложим на составляющие:
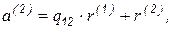
при условии 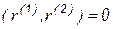 . Умножая это выражение скалярно на
. Умножая это выражение скалярно на 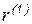 с учетом ортогональности, получаем
с учетом ортогональности, получаем
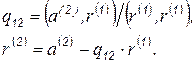
Аналогично вектор 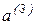 раскладываем на три составляющие:
раскладываем на три составляющие:
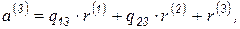
при условиях 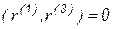 и
и 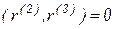 .
.
Последовательно умножая это выражение скалярно на 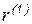 , затем на
, затем на 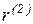 , получим
, получим
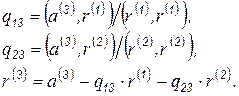
В общем виде, разложение исходных векторов 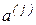 на ортогональные векторы
на ортогональные векторы 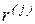 запишем
запишем
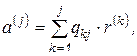 (6.56)
(6.56)
где 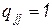 .
.
В соответствии с матричными операциями разложение (6.56) исходной матрицы  соответствует произведению ортогональной матрицы
соответствует произведению ортогональной матрицы 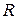 на верхнетреугольную матрицу
на верхнетреугольную матрицу 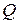 с единичной диагональю.
с единичной диагональю.
Продолжая дальше процесс ортогонализации, приходим к следующей форме записи алгоритма
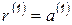 , (6.57)
, (6.57)
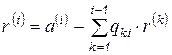 , 6.58)
, 6.58)
где 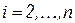 ,
,
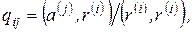 (6.59)
(6.59)
где 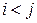 ;
; 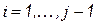 ;
; 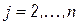 .
.
В результате данного алгоритма окажутся сформированными ортогональная по столбцам матрицам 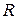 и верхнетреугольная матрица
и верхнетреугольная матрица 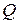 с единичной диагональю.
с единичной диагональю.
Если необходимо получить вместо ортогональной ортонормированную матрицу 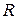 (сумма квадратов элементов столбца равна
(сумма квадратов элементов столбца равна 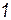 ), то следует нормировать каждый текущий вектор:
), то следует нормировать каждый текущий вектор:
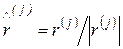 , (6.60)
, (6.60)
где 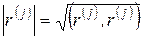 . Заметим также, что скалярное произведение вектора самого на себя равно квадрату длины вектора:
. Заметим также, что скалярное произведение вектора самого на себя равно квадрату длины вектора:
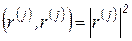 . (6.61)
. (6.61)
В случае нормировки разложение исходных векторов 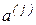 на ортогонормальные векторы
на ортогонормальные векторы 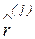 запишется
запишется
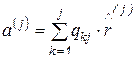 , (6.62)
, (6.62)
где 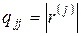 .
.
В соответствии с матричными операциями разложение (6.62) исходной матрицы  соответствует произведению ортонормальной матрицы
соответствует произведению ортонормальной матрицы 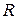 на верхнетреугольную матрицу
на верхнетреугольную матрицу 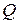 .
.
Процесс ортогонализации и нормировки, соответствующий разложению матрицы  на ортонормальную и верхнетреугольную с учетом (6.57) – (6.59) и (6.60), можно записать соотношениями
на ортонормальную и верхнетреугольную с учетом (6.57) – (6.59) и (6.60), можно записать соотношениями
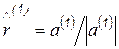 , (6.63)
, (6.63)
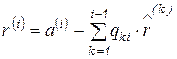 , (6.64)
, (6.64)
где 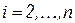 ,
,
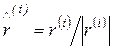 , (6.65)
, (6.65)
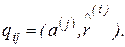 (6.66)
(6.66)
где 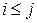 ;
; 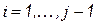 ;
; 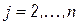 . Этот процесс называется ортогонализацией Грамма-Шмидта.
. Этот процесс называется ортогонализацией Грамма-Шмидта.
Проиллюстрируем разложение матрицы на ортогональную и верхнетреугольную с единичной диагональю на простейшем примере матрицы порядка 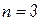 :
:
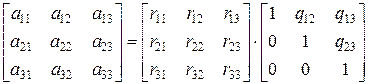 .
.
Зададимся конкретными значениями элементов матрицы
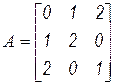 .
.
Согласно алгоритму, полагаем вначале
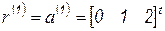 .
.
Тогда
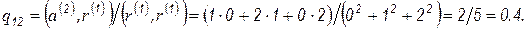
После чего находим
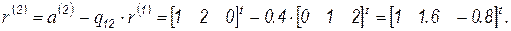
Для определения 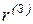 вычисляем
вычисляем
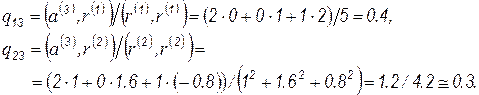
Откуда
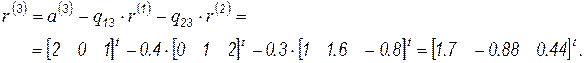
Проверяем результат разложения:
|

|

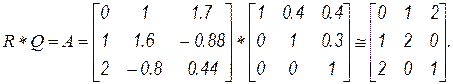
и взаимную ортогональность векторов 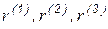
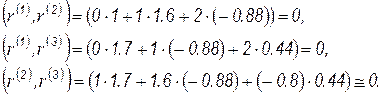
Правильность разложения и ортогональность векторов выполняется, однако векторы не нормированы.
Используя данный пример, рассмотрим процесс разложения матрицы на произведение ортонормальной и верхнетреугольной матриц.
Нормируем первый вектор:
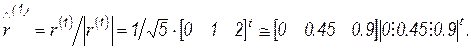
Вычислим
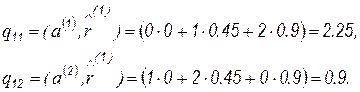
Теперь можем найти
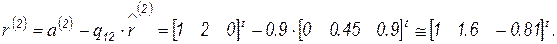
Вычисляем норму
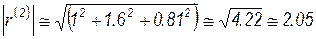
и нормируем вектор
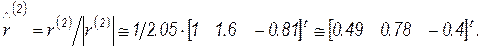
Для определения 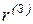 вычислим
вычислим
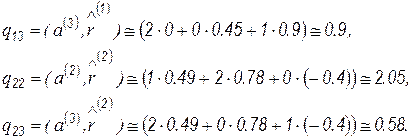
Далее находим
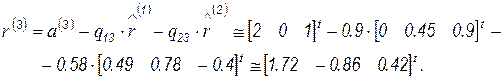
Вычислим норму
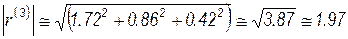
и нормируем вектор
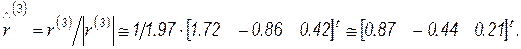
Вычислим
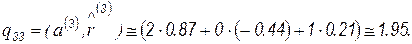
Проверим результат разложения
|

|

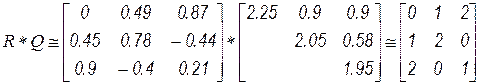
и взаимную ортогональность векторов 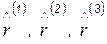
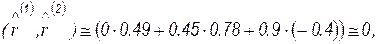
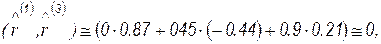

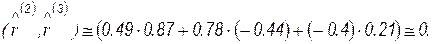
Обратим внимание, что значения матриц 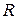 и
и 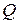 существенно изменились в результате нормировки системы ортогональных векторов.
существенно изменились в результате нормировки системы ортогональных векторов.
Вариант ортогонализации по строкам. Суть алгоритма основана на альтернативном утверждении, что всякую неособенную матрицу  можно представить в виде произведения матрицы
можно представить в виде произведения матрицы 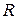 с ортогональными строками и нижнетреугольной матрицы
с ортогональными строками и нижнетреугольной матрицы 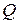 с единичной диагональю либо в виде произведения ортонормальной по строкам матрицы
с единичной диагональю либо в виде произведения ортонормальной по строкам матрицы 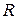 и обычной нижнетреугольной матрицы
и обычной нижнетреугольной матрицы 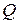 :
:
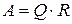 . (6.67)
. (6.67)
Представим исходную матрицу как совокупность векторов-строк
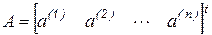 ,
,
где 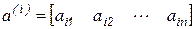 ;
; 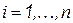 .
.
Т.к. матрица  неособенная, то векторы
неособенная, то векторы 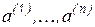 линейно независимы. Будем искать матрицу
линейно независимы. Будем искать матрицу 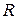 в виде
в виде
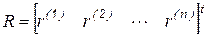 ,
,
где 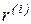 – искомые ортогональные строки.
– искомые ортогональные строки.
Вначале положим 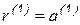 . Следующий вектор
. Следующий вектор 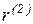 должен быть построен из
должен быть построен из 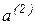 ортогонально
ортогонально 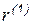 . Для этого вектор
. Для этого вектор 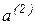 разложим на составляющие:
разложим на составляющие:
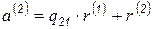 ,
,
где 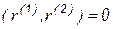 . Умножая это выражение скалярно на
. Умножая это выражение скалярно на 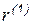 с учетом ортогональности, получаем
с учетом ортогональности, получаем
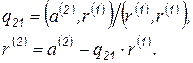
Аналогично вектор 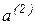 раскладываем на три составляющие:
раскладываем на три составляющие:
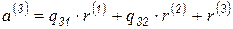 ,
,
при условиях 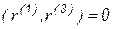 и
и 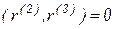 .
.
Последовательно умножая это выражение скалярно на 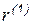 , а затем на
, а затем на 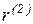 , получим
, получим
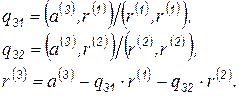
В общем виде разложение исходных векторов 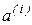 на ортогональные векторы
на ортогональные векторы 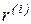 запишется как
запишется как
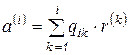 , (6.68)
, (6.68)
где 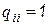 .
.
Матричным операциям разложения (6.68) исходной матрицы  соответствует произведение нижнетреугольной матрицы
соответствует произведение нижнетреугольной матрицы 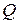 с единичной диагональю на ортогональную матрицу
с единичной диагональю на ортогональную матрицу 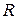 .
.
Продолжая дальше процесс ортогонализации, приходим к следующей форме записи алгоритма:
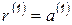 , (6.69)
, (6.69)
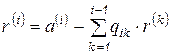 , (6.70)
, (6.70)
где 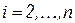 ,
,
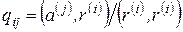 , (6.71)
, (6.71)
где 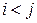 ;
; 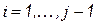 ;
; 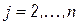 .
.
В результате данного алгоритма окажутся сформированными ортогональная по строкам матрица 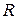 и нижнетреугольная матрица
и нижнетреугольная матрица 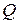 с единичной диагональю.
с единичной диагональю.
В случае нормировки разложение исходных векторов 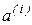 на ортогонормальные вектора
на ортогонормальные вектора 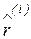 запишется как
запишется как
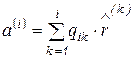 , (6.72)
, (6.72)
где 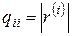 .
.
В соответствии с матричными операциями разложение (6.72) исходной матрицы  соответствует произведению нижнетреугольной матрицы
соответствует произведению нижнетреугольной матрицы 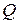 на ортонормальную матрицу
на ортонормальную матрицу 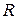 .
.
Процесс ортогонализации нормировки, соответствующий разложению матрицы  на ортонормальную и верхнетреугольную с учетом (6.69)–(6.71) и (6.60), можно записать соотношениями
на ортонормальную и верхнетреугольную с учетом (6.69)–(6.71) и (6.60), можно записать соотношениями
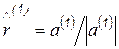 , (6.73)
, (6.73)
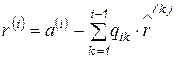 , 6.74)
, 6.74)
где 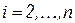 ,
,
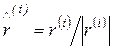 , (6.75)
, (6.75)
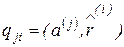 , (6.76)
, (6.76)
где 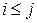 ;
; 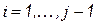 ;
; 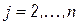 . Этот процесс также соответствует ортогонализации Грамма-Шмидта.
. Этот процесс также соответствует ортогонализации Грамма-Шмидта.
При факторизации матрицы с целью решения линейной системы удобно рассмотреть матрицу, расширенную вектором свободных членов, в качестве (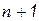 )-го столбца. В результате процесса ортогонализации на месте вектора свободных членов
)-го столбца. В результате процесса ортогонализации на месте вектора свободных членов
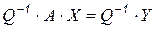
или
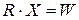 (6.77)
(6.77)
окажется трансформированный вектор 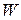 .
.
 2014-02-12
2014-02-12 7594
7594








