Простые методы интегрирования

Основные определения

РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ЭЛЕКТРОННЫХ СХЕМ

Для определения переходного процесса как реакции цепи во времени на реальное воздействие необходимо знать математическую модель цепи в виде системы дифференциальных уравнений (СДУ), описывающих состояние цепи во временной области. Так, для СДУ в нормальной форме Коши разработаны методы аналитического и численного интегрирования, позволяющие находить решение в виде системы функций. Аналитические решения имеют в основном лишь линейные СДУ. Уравнения с периодическими и нелинейными коэффициентами имеют решения в отдельных частных случаях. Поэтому мы будем использовать численные методы интегрирования СДУ, пригодные как для линейных, так и для нелинейных СДУ.

В результате метода конечно-разностного представления компонентных уравнений реактивных элементов, цéпи, содержащие реактивные элементы, преобразуются в цепи с резисторами и источниками. Вычисление переходного процесса представляет процесс итерационного решения алгебраической системы уравнений с подстановкой на каждой итерации текущего решения в качестве предыдущего до тех пор, пока не получим установившееся решение.

Для линейных цепей это сводится к переформированию на каждом шаге итераций вектора правой части, зависящего от предыдущего решения, и повторному решению системы с неизменной матрицей коэффициентов. В этом случае предпочтительны методы, основанные на LU- и QR-факторизации матрицы коэффициентов, позволяющие почти вдвое быстрее получить повторное решение.

Дифференциальное уравнение в нормальной форме Коши, разрешенное относительно производной, можно записать в виде

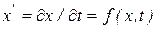, (10.1)

где 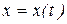– функция времени 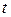. Соответствующий этому уравнению интеграл запишется 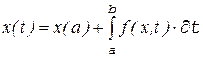, (10.2)

где 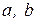– нижний и верхний пределы интегрирования.

Задача численного интегрирования ДУ на каждом шаге интегрирования сводится к нахождению отсчета функции 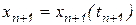в момент времени 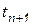при известном значении функции 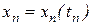в предыдущий момент времени 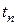и заданном шаге интегрирования 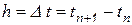. Начальное значения (начальное условие – н.у.) функции 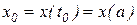находится в момент времени .

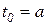При численном методе интегрирования и заданных н.у. найденное значение функции 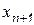в момент времени 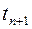, будет отличаться от истинного значения. Ошибка интегрирования будет зависеть от размера шага и метода интегрирования.

Проиллюстрируем на рисунке вывод простых формул численного интегрирования и происхождение погрешностей.

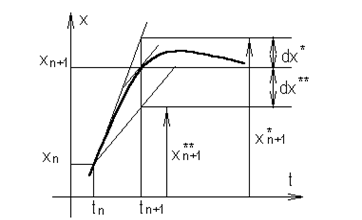
Рис. 10.1 – Иллюстрация простых формул численного интегрирования

Прямая формула Эйлера. По известному значению функции 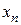в момент времени 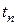найдем приближенное значение 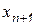(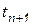), предполагая, что на малом интервале 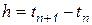наклон функции остается неизменным. Тогда в соответствии с рис. 10.1, Учитывая, что 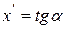, можем записать прямую формулу Эйлера

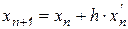. (10.3)

Значение функции в следующей точке вычисляется через значение функции и ее производную в предыдущей точке. Из рисунка видно, ошибка вычисления тем больше, чем больше шаг интегрирования.

Обратная формула Эйлера. Можно выразить значение функции в следующей точке через ее значение в предыдущей точке и значение производной в искомой точке. Как и прежде, полагая, что наклон функции на интервале 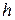остается неизменным и 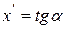, можем записать обратную формулу Эйлера

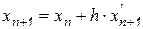. (10.4)

Здесь значение функции 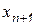в точке 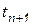входит в правую и левую части выражения (10.4), поскольку 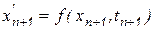, что требует итерационного метода расчета, причем значение в предыдущей точке должно быть известно, а приближенное значение функции в искомой точке предсказано, например, по прямой формуле Эйлера. Тогда в результате итераций по известному приближенному значению функции в искомой точке 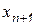и выражению для производной 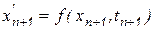находится ее значение с заданной точностью.

Обратную формулу Эйлера можно интерпретировать как выражение значения функции в предыдущей точке через неизвестные значения функции и ее производной в последующей точке

.

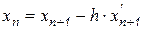Прямую и обратную формулы Эйлера можно записать также в виде

,

.

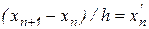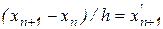Т.е. приращение искомой функции на шаге интегрирования определяется значением производной этой функции в начале либо в конце интервала 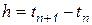. Такая интерпретация прямой и обратной формул Эйлера говорит о возможности получения других конечно-разностных формул интегрирования.

Формула трапеций. Определив приращение искомой функции на шаге интегрирования линейной комбинацией производных 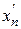и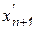

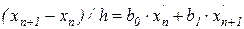
и полагая 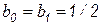, получаем формулу трапеций, являющейся простейшей многошаговой формулой:

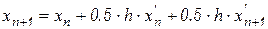. (10.5)

Метод прогноза-коррекции. На основе предсказания значения функции по исходному соотношению 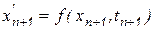можно определить прогноз – грубое значение производной в этой точке и уточнить – скорректировать - это значение, используя обратную формулу Эйлера или формулу трапеций. Т.о., мы приходим к понятию коррекции. По уточненному значению функции можно найти уточненное значение производной и уточнить значение функции с заданной погрешностью. После этого по прямой формуле Эйлера предсказывается значение функции в следующей точке и уточнение повторяется.

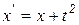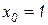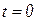Отличия алгоритмов численного интегрирования рассмотрим на примере линейного неоднородного ДУ . Определим н.у. при и шаг 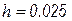. Точное решение этого уравнения имеет вид .

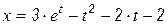1) Прямая формула Эйлера (10.3). В начальный момент времен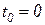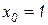и , и 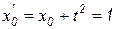. В следующий момент времени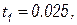

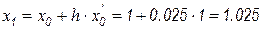
И .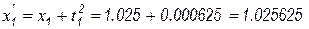

Таблица 10.1 - Результаты интегрирования по прямой формуле Эйлера

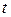
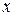
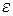
0.000	1.00000	0.00000
0.025	1.02500	–0.00032
	…
0.100	1.1040340	–0.0014788

2) Метод прогноза-коррекции с прогнозом по прямой формуле Эйлера и с коррекцией по обратной. Уточнение будем производить в два этапа.

Пр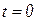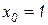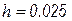и , , , и 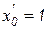, по прямой формуле Эйлера получим 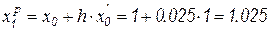. Первая итерация дает скорректированное значение ;

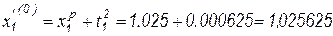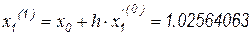
Вторая итерация: ; .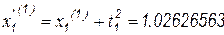

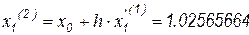Таблица 10.2 – Результаты интегрирования методом прогноз–коррекция

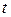
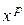
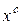
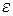
0.000	1.00000	1.02564	0.0
		1.02566
0.025	1.02566	1.02500	0.00034
		1.02502
		…
0.100	1.10707		0.00155

Видно, что для прямой формулы Эйлера ошибки отрицательны, тогда как для метода прогноз-коррекция на основе прямой и обратной формул Эйлера они положительны. Следовательно, комбинация этих двух формул, например формула трапеций, может дать меньшую ошибку.

3) Метод прогноза-коррекции с прогнозом по прямой формуле Эйлера и с коррекцией по формуле трапеций.

Таблица 10.3 – Результаты интегрирования методом трапеций

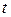
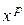
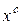
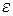
0.000	1.00000	1.025320	0.0
		1.025324
0.025	1.025324	1.051317	0.000004
		1.051321
		…
0.100	1.105530		0.000017

Как видно, ошибка значительно уменьшилась.

Полученные формулы численного интегрирования пригодны как для линейных, так и для нелинейных СДУ.