Модели кластерного анализа

Модели кластерного анализа используются для оптимального (с точки зрения некоторого критерия качества классификации T) разбиения исходного множества реализаций 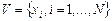на k подмножеств (кластеров) .

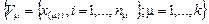Количество k заранее неизвестно, задается только возможный диапазон значений, т.е.,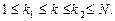

Различают следующие виды моделей кластерного анализа:

· по критерию разделения объектов: дисперсионные, дискриминантные, задачи разделения смесей;

· по алгоритмам решения: детерминированные (используются в предположении четкого разделения классов в пространстве признаков, когда для каждого объекта существует единственное число, характеризующее возможность отнесения его к определенному признаку), стохастические (каждый объект характеризуется различной вероятностью его отнесения к определенному классу, результат решения представляет собой набор этих вероятностей). Статистические модели, в свою очередь, делятся: на параметрические (строятся для количественных признаков), непараметрические (используются для качественных признаков) и аппроксимационные.

В качестве критерия качества разделения объектов на классы Т обычно используется средний по группам разброс реализаций относительно математического ожидания в пределах каждой группы как центра группирования («центра тяжести»):

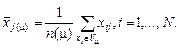(3.6)

При минимизации этого критерия одновременно достигается также и максимизация среднего разброса «центров тяжести» групп относительно общего центра группирования всей совокупности V.

Кластер-анализ, таким образом, позволяет разбивать исследуемую совокупность объектов (значения признаков которых известны) таким образом, чтобы элементы одного класса находились на небольшом расстоянии друг от друга, в то время как разные классы были бы на достаточном удалении друг от друга и не разбивались бы на столь же взаимоудаленные части.