Численное интегрирование

Вычисление определенного интеграла I= 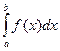геометрически сводится к вычислению площади криволинейной трапеции, ограниченной функцией f(x), осью абсцисс и прямыми х=а и х=b. Численные методы при вычислении интегралов обычно применяются при взятии не берущихся интегралов от достаточно сложных функций, которые предварительно табулируются, а также при интегрировании таблично заданных функций. Все численные методы строятся на том, что подынтегральная функция приближённо заменяется более простой. В результате получаются формулы интегрирования в виде взвешенной суммы ординат функции в отдельных точках:
I= å w_i f(x_i)

Чем меньше интервалы, на которых производят замену, тем точнее вычисляется исходный интеграл. Погрешность численного интегрирования обычно определяется путём двойного интегрирования: с шагом h=(b-a)/n и с шагом, увеличенным в 2 раза. Разница вычисленных значений интегралов определяет погрешность.

Метод трапеции основан на разбиении области интегрирования на большое количество равных маленьких промежутков, замене подынтегральной функции на каждом участке наклонной прямой и вычислении интеграла (площади фигуры), как суммы площадей образующихся трапеций.

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА

ДАНО: f(x) – непрерывная функция. [ a,b ] – отрезок интегрирования.

НАЙТИ: S – значение интеграла. R – погрешность вычислений.

СВЯЗЬ. Пусть N – количество интервалов разбиения отрезка интегрирования. Соединим точки разбиения с графиком функции F(x) и продолжим эти линии так, чтобы получились трапеции, высота которых будет составлять 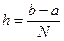, а длины оснований f(xi), где х i – значение i-ой точки разбиения. x1=a, x2=x1+h, x3=x2+h и т.д.

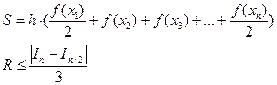
Задание 5.1. Сделать математическую постановку вычисления площадей методами левых, серединных и правых прямоугольников, в которых на отрезках интегрирования подынтегральная функция заменяется горизонтальными прямыми со значением ординаты соответственно слева, в середине и справа участка.

Метод Симпсона базируется на замене подынтегральной функции квадратичной параболой, которая строится на каждом участке по трем точкам (крайние и средняя точки).

При интегрировании полиномов второго порядка получается следующая расчетная формула: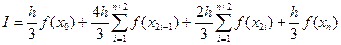

При работе с этим методом интервал надо обязательно разбивать на четное число участков. По сравнению с методами прямоугольников и трапеций метод Симпсона более точный. Погрешность метода можно оценить по соотношению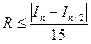

Метод Ньютона-Котеса является обобщением предыдущих и предполагает замену подынтегральной функции параболой k-го порядка. Расчетная формула для одного участка выглядит следующим образом: ,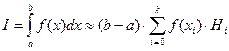

где Н_i – коэффициенты Ньютона-Котеса, x₀ =a, x_n=b, x_i=a+i(b-a)/k

Коэффициенты не зависят от функции и определены заранее:

k=1; H₀= H₁=1/2

k=2; H₀= H₂=1/6; H₁=2/3

k=3; H₀= H₃=1/8; H₁= H₂=3/8

k=4; H₀= H₄=7/90; H₁= H₃=16/45; H₂=2/15

…

При разбиении всего интервала на n участков формулу следует применять для каждого участка, а результаты сложить.

При k=1 получаем метод трапеции, k=2 – метод Симпсона.

Метод Гаусса отличается от предыдущих методов тем, что значения х_i располагаются неравномерно. Предварительно следует преобразовать переменную интегрирования, приведя ее к диапазону [-1,1] следующим образом: 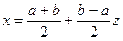. Общая формула интегрирования методом Гаусса выглядит так: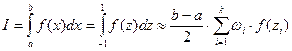

Значения параметров при интегрировании полиномов k-го порядка приведены ниже:

k=2; -z₁=z₂=0,577350; ω₁= ω ₂=1

k=3; -z₁=z₃=0,774597; ω₁= ω ₃=0,555555

z₂ =0; ω ₂=0,888889

k=4; -z₁=z₄=0,861136; ω₁= ω ₄=0,347855

-z₂ = z₃=0,339981; ω ₂= ω ₃=0,652145

…

Этот метод обладает более высокой точностью, хотя и требует более сложных вычислений.

ЗАДАЧА 5.1.

Вычислить интеграл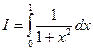

РЕШЕНИЕ.

1. Разобьем интервал на 4 равных участка.

h=0,25; n=4

X	0	0,25	0,5	0,75	1
f(x)=	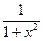1	0,9412	0,8	0,64	0,5

По методу трапеций I=(0,5+0,9412+0,8+0,64+0,25)∙0,25=0,7828

По методу Симпсона I= 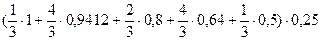=0,7854

2. По формуле Ньютона-Котеса при k=4 и n=1

I= 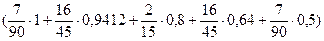= 0,7855

3. По формуле Ньютона-Котеса при k=2 и n=2

I₁=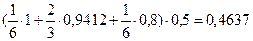

I₂=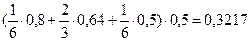

I=I₁+ I₂=0,7854

4. По методу Гаусса при k=4 и n=1

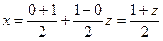
Z	-0,861136	-0,339981	0,339981	0,861136
X	0,0694	0,3300	0,6700	0,9306
f(x)=	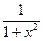0,9952	0,9018	0,6902	0,5359

I=(0,347855∙0,9952+0,652145∙ 0,9018+0,652145∙ 0,6902+ 0,347855∙0,5359) ∙0,5=0,7854

Метод Монте-Карло построен на случайном выборе точек внутри прямоугольника, содержащего заданную фигуру. Идея метода: при большом количестве точек, наугад выбранных внутри прямоугольника, доля точек, содержащихся в заданной фигуре, приближенно равна отношению площади этой фигуры к площади прямоугольника.

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА

ДАНО: f(x) – непрерывная функция.

N – количество случайных точек.

[ а,b ] [ c,d ] – прямоугольник, содержащий фигуру.

НАЙТИ: S – площадь фигуры.

CВЯЗЬ: 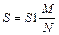, где

S1=(b–a)(d–c) – площадь прямоугольника, содержащего фигуру;

М – число случайных точек с координатами (x,y), попавших в фигуру. Попавшие в фигуру точки определяются одним из приведенных ниже условий.

y f(x)	y f(x)	x2+y2 r2

Задание 5.2. Определить формулы вычисления случайной точки в каждом из трёх приведённых вариантов с помощью функции rnd(1), моделирующей случайное число на отрезке [0,1].

6. Численное решение задач оптимизации.