2014-02-12
1960
В теоретических и математических задачах принято рассматривать задачи оптимизации как задачи поиска минимума функции. Даже методы имеют общее название – методы спуска. Но всегда легко можно перейти от одного вида экстремума к другому путем смены знака у критерия оптимальности.
Рассмотрим задачу вида:
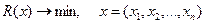
Метод покоординатного спуска (градиента) формирует шаг по переменным как функцию от градиента R(x) в текущей точки последовательности. Градиент – это вектор из частных производных, который показывает направление и скорость возрастания функции.
Алгоритм поиска minR(x) в векторной форме записывается в виде: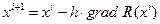 
, или в скалярном виде: 
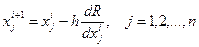, где h – величина рабочего шага, i – номер шага. Поиск максимума можно производить в обратном направлении градиента, т.е. 
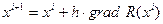или заменить на поиск минимума противоположной функции.
Выбор величины рабочего шага в направлении градиента зависит от величины градиента и сильно влияет на эффективность метода. Существует ряд алгоритмов коррекции величины h. Остановимся на выборе постоянного рабочего шага.
|
|
|
Для оценки частных производных можно применить алгоритм с парными пробами:
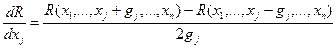, где gj – пробный шаг по j-й переменной, выбираемый достаточно малым.
Условием окончания поиска может являться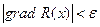 
, где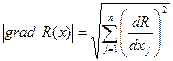 
Основным недостатком метода является необходимость частого вычисления производных.
Метод наискорейшего спуска сочетает в себе метод градиента и методы одномерной оптимизации.
Алгоритм метода:
1. Выбирается начальная точка.
2. В текущей точке вычисляется градиент.
3. В направлении вычисленного градиента ищется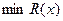 
любым методом одномерной оптимизации. Наиболее часто используется сканирование до первого локального минимума. Полученная точка локального минимума считается следующей точкой последовательности.
4. Повторяются пункты 2 и 3 до выполнения условия окончания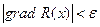
Можно использовать уменьшения рабочего шага после каждой смены направления, чтобы с большей точностью находить оптимум.
ЗАДАЧА 6.2.
Требуется найти минимум функции
1. Рассмотрим метод покоординатного спуска.
Выберем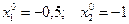 
; h=0,1; g=0,01; ε=0,01
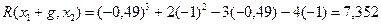
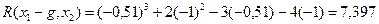
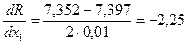
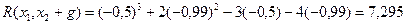
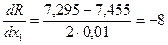
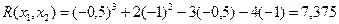
Делаем рабочий шаг и получаем:
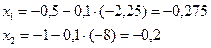
Результаты дальнейших шагов сведем в таблицу:
| № | х1 | х2 | dR/d х1 | dR/d х2 | /gradR/ | R |
| 2 | 0,002 | 0,280 | -2,78 | -4,8 | 5,547 | 1,375 |
| 3 | 0,302 | 0,568 | -2,7258 | -1,7280 | 3,2274 | -2,5060 |
| 4 | 0,575 | 0,741 | -2,0085 | -1,0368 | 2,2603 | -,34002 |
| … | ||||||
| 14 | 1,000 | 0,998 | -0,005 | -0,0063 | 0,0063 | -4,0000 |
Получили grad R(x)=0,0063<0,01, следовательно, поиск можно прекратить.
x1=1; x2=0,998; R(x)=-4
2. При тех же начальных значениях рассмотрим метод наискорейшего спуска.
| № | х1 | х2 | dR/d х1 | dR/d х2 | /gradR/ | R |
| 1 | -0,5 | -1 | -2,25 | -8 | 8,31 | 7,375 |
| 1 | -0,5-0,1(-2,25)= -0,275 | -1-0,1(-8)=-0,2 | -2,25 | -8 | 8,31 | 1,6842 |
| 1 | -0,050 | 0,6 | -2,25 | -8 | 8,31 | -1,5301 |
| 1 | 0,175 | 1,4 | -2,25 | -8 | 8,31 | -2,1996 |
В следующей точке (0,4; 0,2) значение R(x)=-0,256>-2,196. Поэтому в найденной точке снова вычисляем градиент и по нему совершаем шаги до тех пор, пока не найдем наилучшую точку.
|
|
|
| № | х1 | х2 | dR/d х1 | dR/d х2 | /gradR/ | R |
| 2 | 0,175 | 1,4 | -2,9081 | 1,6 | 3,3192 | -2,1996 |
| 2 | 0,466 | 1,24 | -2,9081 | 1,6 | 3,3192 | -3,1811 |
| 2 | 0,757 | 1,08 | -2,9081 | 1,6 | 3,3192 | -3,8239 |
| 2 | 1,047 | 0,92 | -2,9081 | 1,6 | 3,3192 | -3,9804 |
ПРИМЕЧАНИЕ. Если начальная точка выбрана вдали от локального экстремума, то метод спуска может привести к неограниченному убыванию функции.
Задание 6.2.
Закончить поиск минимума по методу наискорейшего спуска.
