а) Для реальных растворов рассмотренные зависимости неприемлемы. Химический потенциал компонента реального газа рассчитывают методом Льюиса. При этом для сохранения формы термодинамических уравнений вместо действительного давления  используют некоторое фиктивное давление газа
используют некоторое фиктивное давление газа 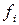 , называемое фугитивностью (летучестью), и подбираемое так, чтобы было справедливо уравнение:
, называемое фугитивностью (летучестью), и подбираемое так, чтобы было справедливо уравнение:
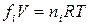 .
.
Тогда
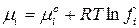 , (101)
, (101)
где 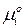 – стандартный химический потенциал индивидуального
– стандартный химический потенциал индивидуального 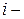 го компонента реальной газовой смеси при данной температуре;
го компонента реальной газовой смеси при данной температуре;
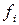 – парциальная фугитивность
– парциальная фугитивность 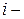 го компонента реальной газовой смеси.
го компонента реальной газовой смеси.
Отношение парциальной фугитивности к парциальному давлению компонента называют коэффициентом фугитивности:
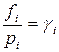 ;
; 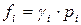 . (102)
. (102)
б) Аналогично, для реальных жидких растворов действительную концентрацию в (100) заменяют соответствующей фиктивной величиной – термодинамической активностью 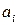 . Термодинамическая активность – относительная безразмерная величина.
. Термодинамическая активность – относительная безразмерная величина.
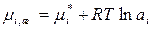 , (103)
, (103)
где 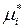 – стандартный химический потенциал чистого
– стандартный химический потенциал чистого 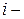 го компонента (
го компонента (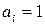 ) в реальной жидкой смеси, зависит от температуры и давления.
) в реальной жидкой смеси, зависит от температуры и давления.
Полученное уравнение позволяет рассчитать 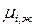 относительно некоторого стандартного состояния. Из (103) имеем:
относительно некоторого стандартного состояния. Из (103) имеем:
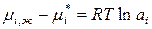 . (104)
. (104)
Физический смысл (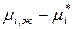 ) – парциальная мольная термодинамическая работа переноса 1 моль
) – парциальная мольная термодинамическая работа переноса 1 моль 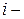 го компонента из данного реального раствора в стандартный раствор.
го компонента из данного реального раствора в стандартный раствор.
Льюис и Рендал связали термодинамическую активность с концентрацией компонентов в растворе через соответствующий коэффициент активности:
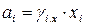 ;
;
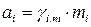 ; (105)
; (105)
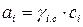 .
.
где 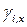 ,
, 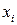 – рациональный коэффициент активности и мольная доля
– рациональный коэффициент активности и мольная доля 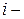 го компонента в растворе, соответственно.
го компонента в растворе, соответственно.
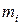 ,
, 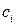 – моляльность (моль/1000 г растворителя) и молярность (моль/дм3)
– моляльность (моль/1000 г растворителя) и молярность (моль/дм3) 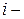 го компонента в растворе;
го компонента в растворе;
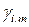 ,
, 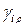 – соответственно, моляльный и молярный коэффициенты активности
– соответственно, моляльный и молярный коэффициенты активности 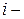 го компонента в растворе.
го компонента в растворе.
Таким образом, 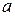 – это “исправленная” концентрация, т.е. та концентрация, которая при подстановке в уравнения для идеальных растворов правильно описывает свойства реальных.
– это “исправленная” концентрация, т.е. та концентрация, которая при подстановке в уравнения для идеальных растворов правильно описывает свойства реальных.
Между 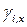 ,
, 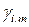 ,
, 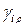 существует вполне определенная взаимосвязь.
существует вполне определенная взаимосвязь.
 2014-02-12
2014-02-12 678
678







