И КОМПОНЕНТА РАСТВОРА
ХИМИЧЕСКИЙ ПОТЕНЦИАЛ ИНДИВИДУАЛЬНОГО ВЕЩЕСТВА
а) На основе термодинамических представлений получим уравнение для химического потенциала индивидуального идеального газа. Из уравнения
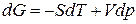 . (83)
. (83)
при постоянной температуре имеем:
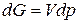 .
.
Учитывая, что для 1 моль индивидуального газа 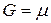 , а для идеального
, а для идеального 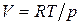 , последнее уравнение преобразуется
, последнее уравнение преобразуется
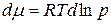 .
.
После интегрирования, получим:
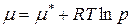 , (92)
, (92)
где 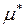 – постоянная интегрирования – функция природы газа и температуры. В стандартных условиях
– постоянная интегрирования – функция природы газа и температуры. В стандартных условиях  атм, тогда из (92) получаем, что в этой системе единиц
атм, тогда из (92) получаем, что в этой системе единиц 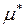 является стандартным химическим потенциалом
является стандартным химическим потенциалом
 .
.
В СИ 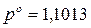 МПа, тогда стандартный химический потенциал равен
МПа, тогда стандартный химический потенциал равен
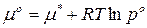 . (93)
. (93)
Вычитая (93) из (92), получим:
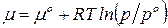 . (94)
. (94)
Если давление выражено в атмосферах, то 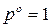 атм., тогда относительное давление
атм., тогда относительное давление 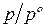 равно фактическому давлению газа, выраженному в единицах атмосферы. Из (94) получим
равно фактическому давлению газа, выраженному в единицах атмосферы. Из (94) получим
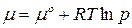 . (95)
. (95)
б) Для химического потенциала 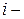 го компонента смеси идеальных газов:
го компонента смеси идеальных газов:
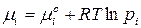 , (96)
, (96)
где 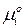 – стандартный химический потенциал индивидуального
– стандартный химический потенциал индивидуального 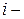 го компонента идеальной газовой смеси при данной температуре;
го компонента идеальной газовой смеси при данной температуре;
 – парциальное давление
– парциальное давление 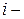 го компонента идеальной газовой смеси, выраженное в тех же единицах, что и стандартное парциальное давление.
го компонента идеальной газовой смеси, выраженное в тех же единицах, что и стандартное парциальное давление.
По закону Дальтона: общее давление идеальной газовой смеси 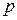 равно сумме парциальных давлений
равно сумме парциальных давлений 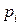 компонентов
компонентов
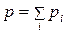 .
.
Парциальное давление 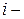 го компонента идеальной газовой смеси – давление, которое оказывал бы газ, если бы он один занимал тот же объем
го компонента идеальной газовой смеси – давление, которое оказывал бы газ, если бы он один занимал тот же объем
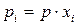 . (97)
. (97)
где 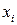 – мольная доля
– мольная доля 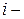 го компонента в идеальной газовой смеси.
го компонента в идеальной газовой смеси.
Подставим в (96) вместо 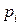 его значение, получим:
его значение, получим:
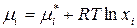 , (98)
, (98)
где 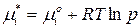 – химический потенциал чистого
– химический потенциал чистого 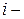 го компонента (
го компонента (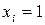 ) в идеальной газовой смеси – функция температуры и общего давления газовой смеси.
) в идеальной газовой смеси – функция температуры и общего давления газовой смеси.
в) Выражение для химического потенциала компонента идеального жидкого раствора, находящегося в равновесии со своим паром, получим из (96)
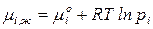 . (99)
. (99)
Основным законом идеальных жидких растворов является эмпирически установленный закон Рауля: парциальное давление компонента над идеальным жидким раствором 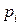 равно произведению давления насыщенного пара чистого (индивидуального)
равно произведению давления насыщенного пара чистого (индивидуального) 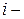 го компонента
го компонента 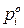 при температуре раствора на мольную долю
при температуре раствора на мольную долю 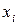 этого компонента в жидком растворе
этого компонента в жидком растворе
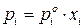 .
.
Подставим в (99) вместо 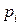 его значение, в результате получим:
его значение, в результате получим:
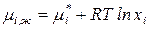 , (100)
, (100)
где 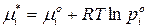 – стандартный химический потенциал чистого
– стандартный химический потенциал чистого 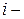 го компонента (
го компонента (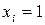 ) в идеальной жидкой смеси, зависит от температуры и давления.
) в идеальной жидкой смеси, зависит от температуры и давления.
 2014-02-12
2014-02-12 870
870








