2014-02-12
609
Метод Крамера (определителей) решения систем линейных уравнений
Правило (метод) Крамера применяется к системам, у которых число уравнений равно числу неизвестных. Этот метод использует определители.
Рассмотрим систему линейных уравнений
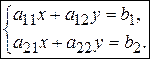
Вычисляются определители:
, 
, 
.
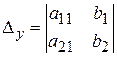Здесь
- определитель системы, составленный из коэффициентов при неизвестных;
- это определитель, полученный из определителя 
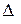заменой столбца коэффициентов при 
на столбец свободных членов;
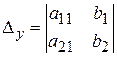- это определитель, полученный из определителя 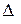заменой столбца коэффициентов при 
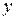на столбец свободных членов.
1. Если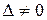 
, то система совместная и определенная, то есть имеет единственное решение, которое находится по формулам Крамера:
.
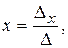
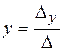2. Если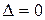 
, а хотя бы один из определителей 
, 
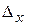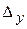отличен от нуля, то система не имеет решений (несовместная).
3. Если 
, то система имеет бесконечно много решений (совместная и неопределенная).
Пример 1. Решить с помощью метода Крамера систему уравнений
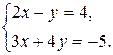
Решение
, поэтому СЛУ имеет единственное решение.
|
|
|
, 
.
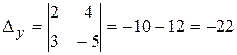Тогда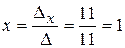 
; 
.
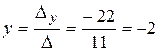Ответ: система уравнений совместна и определенна, ее единственное решение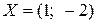 
.
Пример 2. Решить с помощью метода Крамера систему уравнений
.
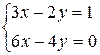Решение
Определитель системы равен нулю: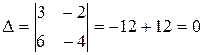 
, однако один из вспомогательных определителей не равен нулю: 
, значит, СЛУ не имеет решений, то есть СЛУ несовместная.
Пример 3. Решить с помощью метода Крамера систему уравнений
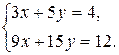
Решение
, 
, 
.
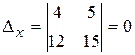Поэтому система имеет бесконечно много решений.
Разделив коэффициенты 2-го уравнения на 3, получим: 
Оставим только одно из этих уравнений: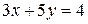 
.
Выразим 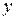через : 
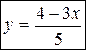, значение - любое действительное число. Это и есть выражение для общего решения СЛУ. Ответ можно записать так: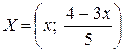 
, где 
.
Придавая различные значения, будем получать бесконечное множество частных решений. Например, при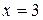 
получим 
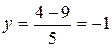и первое частное решение 
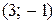. При 
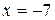получим 
и второе частное решение 
, и так далее.
