2014-02-12
467
Первый шаг метода Гаусса - исключение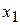 
из всех уравнений, кроме первого.
Предположим, что коэффициент при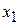 
в первом уравнении не равен нулю (
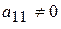). Оставляя неизменным первое уравнение (оно будет ведущим), выполним элементарные преобразования так, чтобы коэффициенты при 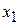в других уравнениях обратились в нули:
А) умножим 1-ое уравнение на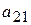 
, а 2-е уравнение – на 
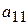, тогда коэффициенты при 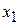в 1-ом и во 2-ом уравнении станут одинаковыми. Затем вычтем из 2-ого уравнения 1-ое и запишем результат вместо 2-го уравнения (в нем 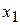будет отсутствовать);
Б) умножим 1-ое уравнение на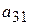 
, а 3-е уравнение – на 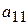, тогда коэффициенты при 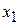в 1-ом и в 3-ом уравнении станут одинаковыми. Затем вычтем из 3-го уравнения 1-ое уравнение. Запишем результат вместо 3-го уравнения (в нем 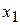будет отсутствовать). И так далее.
Получим:
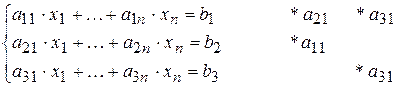
Получим систему вида
Второй шаг метода Гаусса - исключение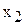 
из уравнений, следующих за вторым уравнением. Далее повторяем эти же действия для 2-го ведущего уравнения системы. Затем – для 3-его. И так далее.
Пример 1. Решить систему линейных уравнений методом исключения неизвестных (Гаусса).
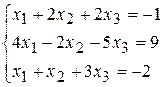
Решение
Шаг 1.
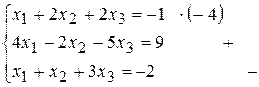
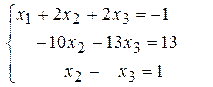
Шаг 2.
+ 
,
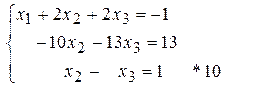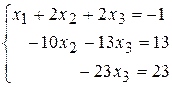В процессе элементарных преобразований с каждой неизвестной СЛУ приведена к треугольному виду.
Шаг 3. Значения неизвестных находятся поочередно из последнего уравнения, предпоследнего и т.д. до первого уравнения. Указанное действие называется обратным ходом Гаусса.
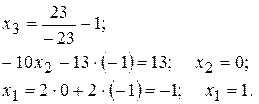
Система имеет единственное решение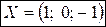 
.
Вывод. Если в процессе элементарных преобразований СЛУ приведена к треугольному виду, то такая СЛУ имеет единственное решение.
